Inhaltsverzeichnis
Nachfolgend eine sinnbildliche Fotomontage einer Hochhaus-Torsion:
Eine Torsionsbeanspruchung liegt vor, wenn ein Bauteil wie Stab oder Welle durch ein Moment (Drehmoment bzw. Torsionsmoment $M_T$) belastet wird, welches um deren Längsachse wirkt. Infolgedessen kommt es zu einer Verdrehung, Verdrillung oder Verwindung des Stabes. Da die Berechnung von Torsion unterschiedlicher Querschnittsformen sehr rechenintensiv ist, wird sich im Rahmen dieses Kurses auf kreisförmige Querschnitte beschränkt. Ferner werden zusätzliche Annahmen getroffen:
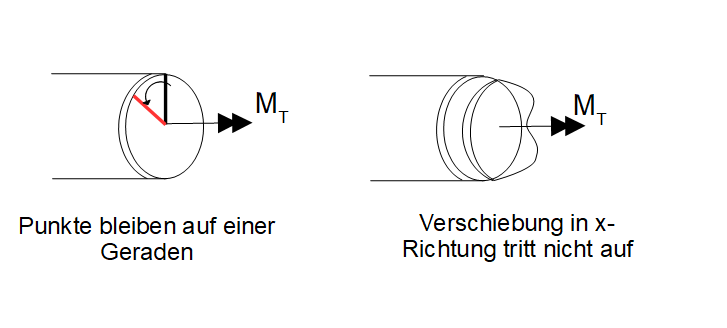
- Die Querschnitte verdrehen sich wie starre Scheiben gegeneinander, d. h. es findet keine Verzerrung der Querschnitte statt. Punkte, die sich vor der Verformung auf einer Geraden befanden, liegen auch nach der Verformung auf einer (anderen) Geraden. -> Querschnitte verformen sich nur um einen Winkel $\varphi$.
- Die Querschnitte bleiben trotz Torsion eben, d. h. es treten keine Querschnittsverwölbungen auf. Infolge der Torsion erfährt der Stab keine Verschiebung in Richtung der Längesachse ($x$-Richtung).
Außerdem:
- Die Berechnung liegt im Geltungsbereich des Hookeschen Gesetzes, d. h. also die Gleichung $\gamma$ ist proportional.
- Spannungen liegen weiterhin im elastischen Bereich [keine nachhaltige plastische Verformung],
- Spannungsüberhöhungen infolge von Löchern oder Kerben können unter Verwendung von Kerbfaktoren in der Rechnung berücksichtigt werden.
Hinweis
In den nachfolgenden Berechnungen werden die Herleitungen an einem Kreisquerschnitt durchgeführt.
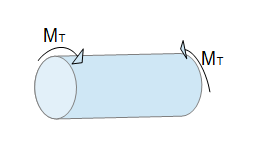
Der erste Untersuchungsgegenstand bei der Untersuchung von Torsion ist eine Welle mit einem konstanten Querschnitt über die gesamte Länge. Es handelt sich um eine Vollwelle, die an beiden Seiten durch das Torsionsmoment $ M_T $ belastet wird.
Merke
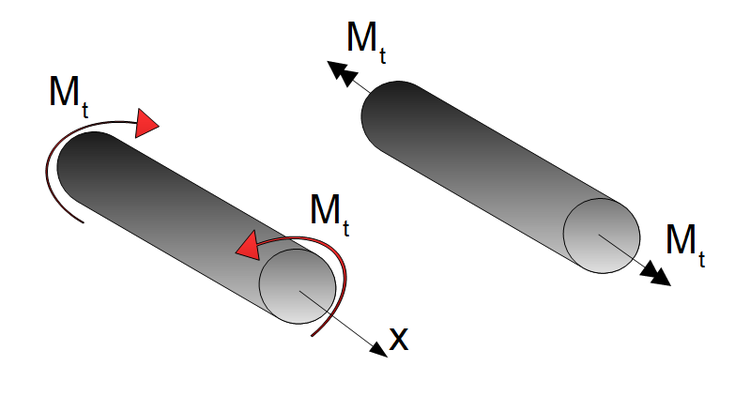
Das Torsionsmoment $M_T$ ist positiv, wenn $M_T$ am positiven Schnittufer als Rechtsschraube um die Stabachse ($x$-Achse) dreht (siehe obige Grafik). Das positive Torsionsmoment wird als Doppelpfeil in Richtung der positiven $x$-Achse (nach rechts gerichtet) angegeben.
Führt man nun einen senkrechten Schnitt durch die Welle, so liegt an dieser Stelle ausschließlich das innere Torsionsmoment $M_T$ vor. Dieses führt zu Schubspannungen in der Schnittebene.
Gegenstand dieser Untersuchung ist die Ermittlung der Spannungsverteilung im Inneren, die Verformung und die Verdrehung der Wellenenden gegeneinander.
Merke
Die Berechnung wird in drei Teile zerlegt:
Statik (Gleichgewichtsbedingungen), kinematische Gleichungen (Verformungen) und das Stoffgesetz (Hookesches Gesetz).
Gleichgewichtsbedingungen
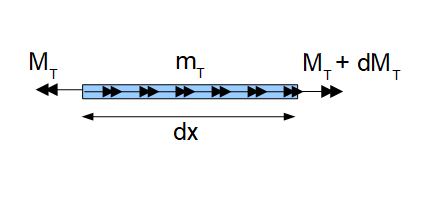
Die Aufstellung der Gleichgewichtsbedingung in $x$-Richtung führt auf die Differentialgleichung 1. Ordnung:
$\rightarrow : -M_T + m_T \cdot dx + (M_T + dM_T) = $
Es folgt:
Methode
$\frac{dM_T}{dx} = M_T' = -m_T$
Kinematische Gleichungen
Aus den oben getroffenen Annahmen, dass die Querschnitte unverformt und eben bleiben, kann man Folgendes ableiten:
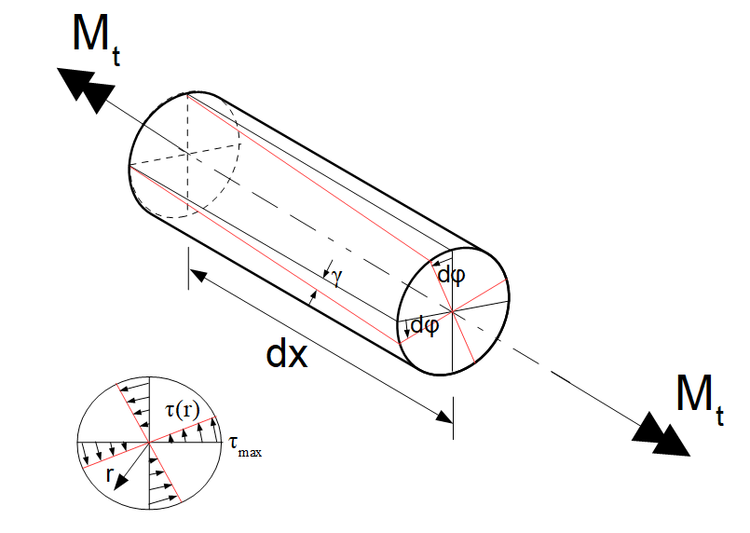
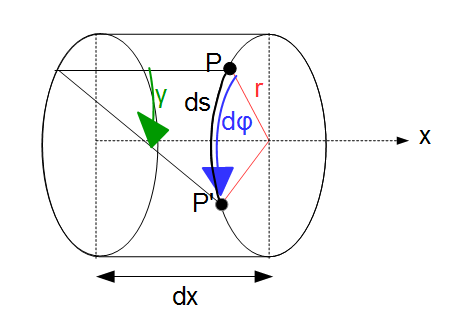
Wir betrachten ein herausgeschnittenes Element der Länge $dx$ der Welle:
- Die 1. Annahme führt dazu, dass sich ein beliebiger Punkt im Querschnitt auf einer Kreisbahn um die Drehachse verschiebt. Die Drehachse verläuft durch den Kreismittelpunkt.
- Ein Punkt leg, t auf der rechten Querschnittsfläche der entnommenen Scheibe, einen Weg $ ds = r d\varphi $ zurück, analog dazu auf der linken Querschnittsfläche in entgegengesetzter Richtung. $r $ steht hierbei für einen beliebigen Radius.
- Alternativ lässt sich der Weg eines Punktes auch mithilfe des Winkels $\gamma$ bestimmen. Siehe hierzu die obige Abbildung. Es gilt: $ r d\varphi = \gamma dx $.
Stellt man diese Gleichung um, erhält man:
$\frac{d\varphi}{dx} = \frac{\gamma_a}{r}$
Auf der linken Seite der Gleichung steht nun der Ausdruck für die Ableitung des Verdrehwinkels $\varphi $ nach $x$. Diesen Ausdruck bezeichnet man auch als Verdrillung $\varphi' $ bzw. $\vartheta$:
Methode
$\varphi' = \vartheta = \frac{d\varphi}{dx} $ Verdrillung
Der Zusammenhang zwischen Gleitwinkel $\gamma $ und Schubspannung $\tau $ lässt sich unter Verwendung des Hookeschen Gesetzes ermitteln:
$\tau = G \gamma = G \; \vartheta \; r $
Merke
Diese Gleichung zeigt, dass eine Zunahme des Radius $ r $ auch zu einer linearen Zunahme der Schubspannungen führt. Daher sind die Schubspannungslinien konzentrische Kreise.
Bestimmung der Verdrillung
Um nun eine genaue Aussage bezüglich der Schubspannung treffen zu können, ist es vorab notwendig die Verdrillung $\vartheta = \varphi'$ zu bestimmen, da diese noch unbekannt ist.
Davon ausgehend, dass die Schubspannungen Momente hervorrufen, integriert man diese über die gesamte Kreisfläche. Als Resultat erhält man dann das resultierende Schnittmoment, welches dem äußeren Moment $ M_T $ entspricht:
$ M_T = \int_A \tau\; r \; dA = \int_A G \vartheta \; r \; dA = G \vartheta \int_A r^2 dA $
Hierbei stellt der Ausdruck $\int_A r^2 = I_P $ das polare Flächenträgheitsmoment dar, womit sich die obige Gleichung umschreiben lässt, zu:
$ M_T = G\; I_p \; \vartheta $.
Löst man diese Gleichung nun noch nach $\varphi' $ auf, so liefert dies die Verdrillung mit:
Methode
$\vartheta = \varphi' = \frac{M_T}{G I_P} $ Verdrillung
mit
$M_T$ Torsionsmoment
$G$ Schubmodul
$I_P$ polares Flächenträgheitsmoment
Es stellt sich nun heraus, dass die Verdrillung von drei Parametern abhängt:
1. Torsionsmoment $ M_T $,
2. Materialparameter $ G $,
3. Polares Flächenträgheitsmoment $ I_P$.
Bestimmung der Schubspannung
Für die vom Radius abhängige Spannung erhält man durch Einsetzen von
$\vartheta = \frac{M_T}{G I_P}$
in
$\tau = G \gamma = G \; \vartheta \; r $
den Ausdruck
Methode
$\tau(r) = \frac{M_T}{I_P} \cdot r $ Schubspannungen
Berechnung der Verdrehung
Wenn in einem zylindrischen Stab an jeder Stelle ein identisches Torsionsmoment wirkt, so ist die Verdrillung $\varphi' = \vartheta$ durchweg konstant.
$\vartheta = \text{konstant}$
$\vartheta = \frac{d\varphi}{dx}$
Trennung der Veränderlichen:
$\vartheta \; dx = d\varphi$
Intergation, wobei $\vartheta = const$:
$\vartheta \int_0^x d_x = \int_{\varphi_0}^{\varphi(x)} d\varphi$
$\vartheta \cdot x = \varphi(x) - \varphi_0$
Methode
$\rightarrow \varphi(x) = \varphi_0 + \vartheta \cdot x $ Verdrehung
Für $x = l$ (Wellenende) gilt dann:
$\varphi(l) = \varphi_0 + \vartheta \cdot l $
Die Anfangsverdrehwinkel $\varphi_0 $ sind dann entsprechend
$\varphi_0 = \varphi(x=0) $.
Merke
Die Quintessenz ist somit, dass die Verdrehung linear zunimmt. Die Verdrehung von einer Wellenseite [$x = 0$ hier Wellenanfang] zur anderen Wellenseite [$x=l$ hier Wellenende] nimmt um $\vartheta \cdot l$ zu.
Die Differenz aus beiden Wellenenden wird beschrieben durch:
$\triangle \varphi = \varphi(l) - \varphi_0$
$\triangle \varphi = \vartheta \cdot l $
Setzt man nun noch den Ausdruck für die Verdrillung $ \vartheta $ ein, liefert dies:
Methode
$\triangle \varphi = \frac{M_T \cdot l}{G \cdot I_P} $ Endverdrehung bei konstanter Verdrillung
Ist die spezifische Verdrehung (bzw. Verdrillung) $\triangle \varphi$ nicht konstant, so kann die Lösung mit Hilfe von Integration erfolgen. Es gilt:
$\vartheta = \frac{d\varphi}{dx}$
Einsetzen in (wobei $\vartheta$ nicht mehr konstant ist):
$\vartheta = \frac{M_T}{G I_P} $
Ergibt:
$\frac{d\varphi}{dx} = \frac{M_T}{G I_P}$
Methode
$\varphi' = \frac{M_T}{G I_P}$ Verdrehung
Mittels Integration kann dann die Verdrehung an einer beliebigen Stelle bestimmt werden:
Methode
$\varphi(x) = \varphi_0 + \int_0^x \frac{M_T(x)}{G(x)I_P(x)} dx $
Bestimmung des polaren Flächenträgheitsmoments
Das polare Flächenträgheitsmoment ist nur dann veränderlich, wenn auch der Durchmesser der Welle variiert.
Für das polare Flächenträgheitsmoment gilt:
Methode
$ I_P = \int_A r^2 dA = \int_{r=0}^r r^2 2\pi r \; dr = \frac{\pi r^4}{2} $ polares Flächenträgheitsmoment
Bestimmung der Maximalspannung
Die maximale Spannung liegt am Rand der Welle. Davon ausgehend, dass der Radius die Länge $r =R$ besitzt, folgt:
Methode
$\tau_{max} = \tau_{r} = \frac{M_T}{I_P}\cdot R $ Maximale Schubspannung
Widerstandsmoment
Eine andere Möglichkeit zur Bestimmung der maximalen Spannung ist die Hinzunahme des Widerstandsmoments $W_T$:
Methode
$ \tau_{max} = \frac{M_T}{W_T} $ Maximale Schubspannung (Widerstandsmoment)
mit
$W_T = \frac{I_P}{R} = \frac{\pi r^3}{2}$
Weitere interessante Inhalte zum Thema
-
Torsion bei Welle mit Kreisquerschnitt
Vielleicht ist für Sie auch das Thema Torsion bei Welle mit Kreisquerschnitt (Torsion) aus unserem Online-Kurs Technische Mechanik 2: Elastostatik interessant.