Inhaltsverzeichnis
In diesem Kurstext gehen wir auf die magnetische Feldstärke und das Durchflutungsgesetz ein.
Magnetische Feldstärke
Ein magnetisches Feld entsteht, sobald ein elektrischer Strom fließt. Die Feldgröße, die dieses Phänomen beschreibt, ist die magnetische Feldstärke $ H $. Sie wird als Vektor dargestellt, da die Feldlinien unterschiedliche Positionen und unterschiedliche Richtungen aufweisen.
Betrachtet man einen elektrischen Leiter, in dem eine Ladungsbewegung stattfindet, so liegt um diesen Leiter herum ein magnetisches Feld dessen Stärke als Feldstärke bemessen wird. Da die Intensität dieses Feldes mit Abstand zum Leiter radial abnimmt, verringert sich auch die magnetische Feldstärke mit zunehmender Entfernung zum Leiter.
Merke
Die Rate mit der dies geschieht, entspricht $\frac{1}{r} \rightarrow r = $ Radius.
Magnetische Feldstärke außerhalb des Leiters:
Die magnetische Feldstärke außerhalb des Leiters berechnet sich durch:
Methode
Magnetische Feldstärke innerhalb des Leiters:
Bei der Berechnung der magnetischen Feldstärke innerhalb eines Leiters wird nur der Strom erfasst, der vom Integrationsweg umschlossen ist.
Methode
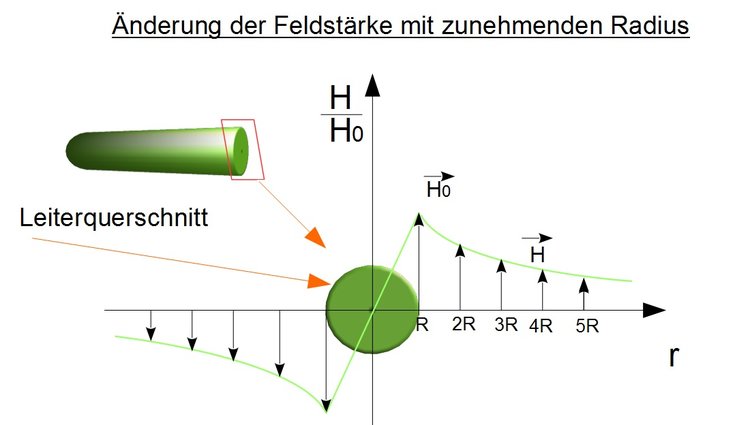
In der nächsten Abbildung ist eine mögliche magnetische Feldstärke für einen Leiter dargestellt.
Man sieht, dass die Feldstärke am Rand des Leiters einen maximalen Wert $ \vec{H_0} $ aufweist. Im Mittelpunkt des Leiters nimmt die Feldstärke den Wert null an. Vergrößert man den Radius über den Wert $ R $ hinaus, so nimmt die Feldstärke kontinuierlich ab.
Durchflutungsgesetz
Merke
Wenn man den Weg, der den Leiter umschließt, definiert, so muss die Integration der Feldstärke auf diesem Weg die Durchflutung ergeben. Dabei ist die Form des Weges oder die Art des Verlaufs entlang von Feldlinien unerheblich. Es muss lediglich gewährleistet sein, dass er in sich geschlossen ist. Daher verwendet man für das Durchflutungsgesetz anstelle eines normalen Integrals ein Kreisintegral $\oint $.
Methode
Aus dem Durchflutungsgesetz lässt sich ablesen, dass die Einheit der magnetischen Feldstärke $ \frac{A}{m} $ ist.
Weitere interessante Inhalte zum Thema
-
Elektrischer Strom
Vielleicht ist für Sie auch das Thema Elektrischer Strom (Gleichstrom) aus unserem Online-Kurs Elektrotechnik interessant.
-
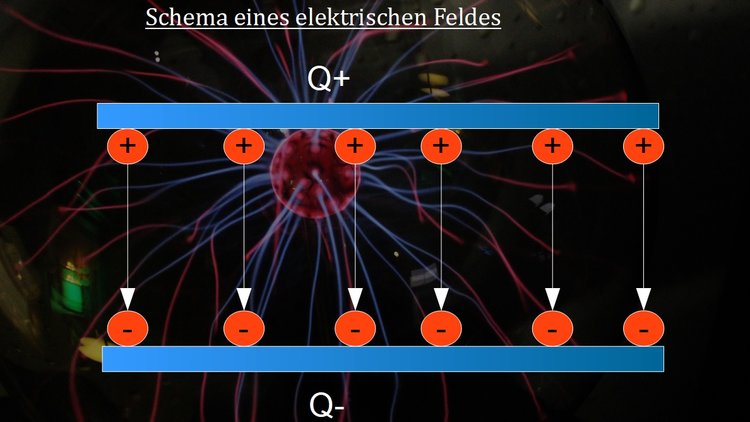
Einführung Elektrisches Feld
Vielleicht ist für Sie auch das Thema Einführung Elektrisches Feld (Elektrisches Feld) aus unserem Online-Kurs Elektrotechnik interessant.