Trigonometrische Funktionen (gr. trigonon = Dreieck, gr. metron = Maß), auch Winkelfunktionen genannt, dienen in der Mathematik zur Berechnung der Zusammenhänge zwischen Winkeln und Seitenverhältinissen. In den Naturwissenschaften dienen sie als fundamentale Funktionen zur Berechnung periodischer Vorgänge.
Die wichtigen trigonometrischen Funktionen sind:
- Sinusfunktion: $f(x) = sin(x)$
- Kosinusfunktion: $f(x) = cos(x)$
- Tangensfunktion: $f(x) = tan(x) = \frac{sin(x)}{cos(x)} $
sowie deren Kehrwerte:
- Kosekansfunktion: $f(x) = csc(x) = \frac{1}{sin(x)} \;\; \longrightarrow$ Kehrwertfunktion der Sinusfunktion
- Sekansfunktion: $f(x) = sec(x) = \frac{1}{cos(x)} \;\; \longrightarrow$ Kehrwertfunktion der Kosinusfunktion
- Kotangensfunktion $\ f(x) = cot(x) = \frac{1}{tan(x)} = \frac{cos(x)}{sin(x)} \longrightarrow$ Kehrwertfunktion der Tangensfunktion
Hinweis
Bitte verwechsle nicht eine Kehrwertfunktion mit einer Umkehrfunktion!
Der Kehrwert ist das Reziproke des Ausgangswertes, eine Kehrwertfunktion entsprechend die reziproke Funktion zur Ausgangsfunktion:
$\to f(x) = sin(x) \Longrightarrow k(x) = \frac{1}{sin(x)} = csc(x)$
Bei einer Umkehrfunktion sind Ziel- und Definitionsmenge gegenüber der umkehrbaren Ausgangsfunktion vertauscht:
$\to f(x) = sin \Longrightarrow f'(x) = arcsin$
Winkelfunktionen am Einheitskreis
In früheren Zeiten waren die trigonometrischen Funktionen nur für Winkel von $0°$ bis $90°$ definiert, da sie nur die Seitenverhältnisse in rechtwinkligen Dreiecken betrachteten.
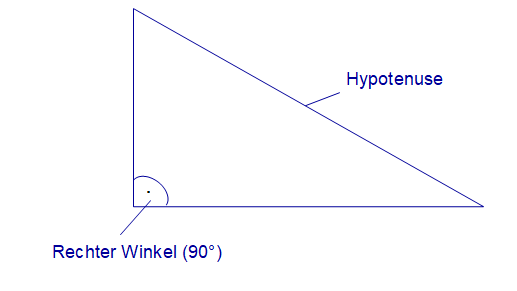
Beispiel
Gegeben sei ein rechtwinkliges Dreieck mit den Seiten $a$, $b$ und $c$ sowie den Winkeln $\alpha$, $\beta$ und $\gamma$. Die Seite $a$ liegt gegenüber $\alpha$, $b$ gegenüber $\beta$ und $c$ gegenüber $\gamma$.
$\longrightarrow sin\alpha = \frac{Gegenkathete von \alpha}{Hypothenuse} = \frac{a}{c}$
Du erinnerst aus der Schule...
Wir können jedoch den Definitionsbereich der Winkelfunktionen erweitern, indem wir sie als Sekanten- und Tangentenabschnitte am Einheitskreis (ein Kreis mit dem Zentrum im Koordinatenursprung mit Radius $1$) berechnen. So sind uns nicht nur alle Winkel bis $360°$, sondern auch negative Winkel zugänglich.
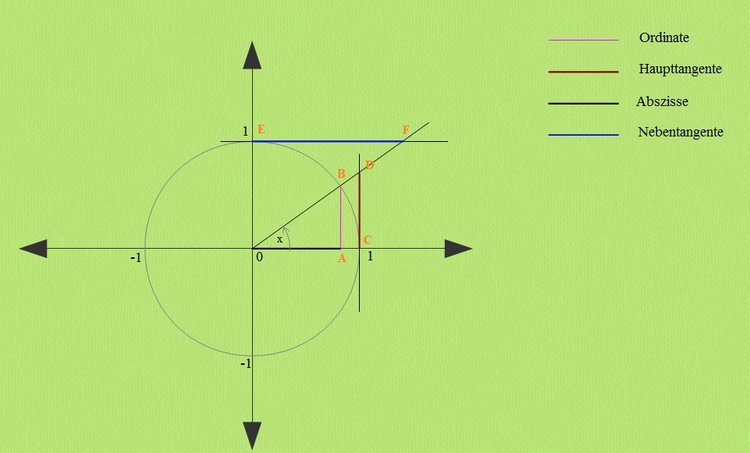
Berechnung am Einheitskreis:
Merke
Sinusfunktion:
Ordinate von B: $y = sin \alpha = |\overline{AB}|$
Kosinusfunktion:
Abszisse von B: $y = cos \alpha = |\overline{0A}|$
Tangensfunktion:
Haupttangentenabschnitt: $y = tan \alpha = \frac{sin(\alpha)}{cos(\alpha)} = |\overline{CD}|$
sowie
Kosecansfunktion:
Abstand vom Koordinatenursprung: $y = csc \alpha = |\overline{0F}|$
Secansfunktion:
Abstand vom Koordinatenursprung: $y = sec \alpha = |\overline{0D}|$
Kotangensfunktion:
Nebentangentenabschnitt: $y = cot \alpha = \frac{cos(\alpha)}{sin(\alpha)} = |\overline{EF}|$
Hinweis
In den weiteren Kurstexten werden wir uns nur mit den wichtigen trigonometrischen Funktionen wie der Sinus-, der Kosinus-, der Tangens- sowie der Kotangensfunktion befassen.
Berechnung eines Punktes auf dem Einheitskreis
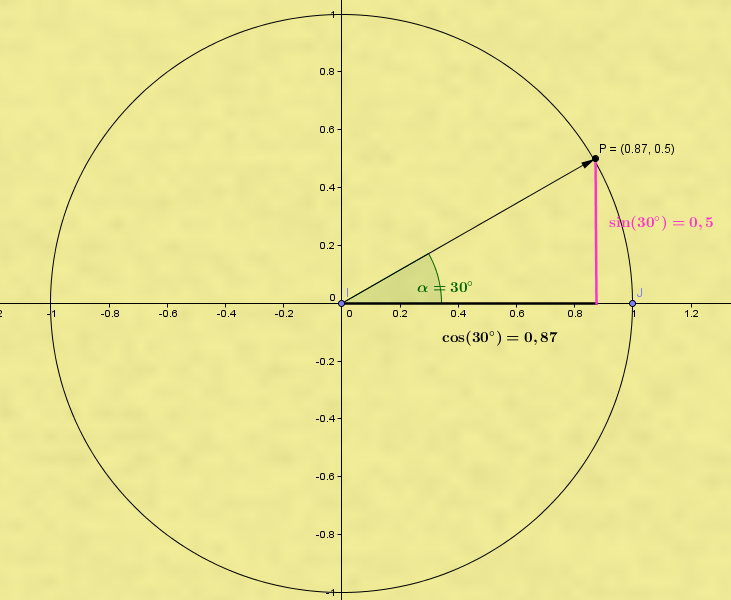
Zu jedem Winkel $\alpha$ zwischen $0°$ und $360°$ gehört ein Punkt $P$ auf dem Einheitskreis mit den Koordinaten $(x, y)$.
Beispiel
$cos(30°) = \frac{1}{2} \sqrt{3} \approx 0,87 \rightarrow x = 0,87$
$sin(30°) = 0,5 \rightarrow y = 0,5$
Die Koordinaten des Punktes lauten: $P(0,87|0,5)$
Weitere interessante Inhalte zum Thema
-
Trigonometrie am rechtwinkligen Dreieck
Vielleicht ist für Sie auch das Thema Trigonometrie am rechtwinkligen Dreieck (Grundlagen der Technischen Mechanik) aus unserem Online-Kurs Technische Mechanik 1: Statik interessant.
-
Harmonische Funktionen
Vielleicht ist für Sie auch das Thema Harmonische Funktionen (Testfunktionen) aus unserem Online-Kurs Regelungstechnik interessant.