Zwischen den trigonometrischen Funktionen bestehen enge rechnerische Beziehung. Eine Funktion würde schon ausreichen, um jedwedes trigonometrische Problem zu berechnen. Zur Vereinfachung können jedoch mehrere verschiedene Kreisfunktionen verwendet werden. Falls es die Rechnung erfordert, können diese auch in einander überführt werden. Im Folgenden stellen wir dir die wichtigsten Beziehungen kurz vor.
Komplementbeziehungen
Wir können mit den Komplementbeziehungen in einem rechtwinkligen Dreieck den Sinus, Kosinus, Tangens usw. eines unbekannten Winkels $\beta$ mit Hilfe eines bekannten Winkels $\alpha$ bestimmen. Die Komplementbeziehungen (lat. komplementum = Abschluss) bezeichnen die Beziehungen zweier Winkel, die addiert $90°$ ergeben:
$\alpha + \beta = 90°$
Ziehen wir in einem rechtwinkligen Dreieck den rechten Winkel von der Innenwinkelsumme eines Dreiecks von $180°$ ab, so sehen wir, dass die beiden anderen Winkel im rechtwinkligen Dreieck in ihrer Summe $90°$ ergeben:
$180° - 90° = 90° = \alpha + \beta$
Daraus ergibt sich:
$\beta = 90° - \alpha$
$\Longrightarrow \, 90° = \alpha + (90° - \alpha)$
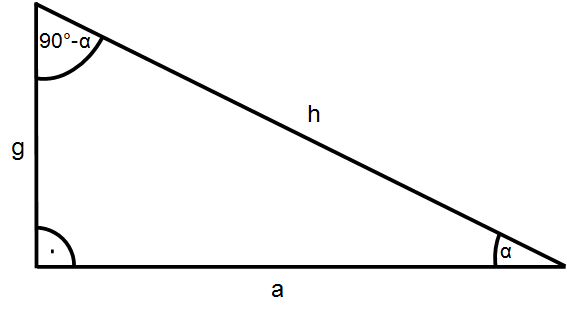
Somit können wir $\beta$ in den folgenden Betrachtungen durch $90° - \alpha$ ersetzen, wie Du auch in der folgenden Abbildung erkennen kannst.
Die Komplementbeziehungen können wir uns bildlich vor Augen führen, indem wir die Innenwinkel und Seiten eines rechtwinkligen Dreiecks betrachten.
Somit gilt für die Innenwinkelsumme:
$\longrightarrow \;180° = 90° + \alpha + (90° - \alpha) \;\;\;$
Den Sinus anwenden ergibt:
$\, sin (\alpha) = \frac{Gegenkathete}{Hypothenuse} = \frac{g}{h}$
$\, cos (90° - \alpha) = \frac{Gegenkathete}{Hypothenuse} = \frac{g}{h}$
$\, \Longrightarrow sin (\alpha) = cos (90° - \alpha)$
Genauso gilt für den Kosinus:
$\, cos (\alpha) = \frac{Ankathete}{Hypothenuse} = \frac{a}{h}$
$\, sin (90° - \alpha) = \frac{Ankathete}{Hypothenuse} = \frac{a}{h}$
$\, \Longrightarrow cos (\alpha) = sin (90° - \alpha)$
Für Tangens und Cotangens folgt:
$\longrightarrow tan (\alpha) = \frac{sin (\alpha)}{cos (\alpha)} \;$ und $\; cot (\alpha) = \frac{cos (\alpha)}{sin (\alpha)}$
$\, \Longrightarrow tan (\alpha) = cot (90° - \alpha)$ $, \;\;\; D(f) = \alpha \neq k \cdot 90° \,| k \in \mathbb{Z}$
$\, \Longrightarrow cot (\alpha) = tan(90° - \alpha)$ $, \;\;\; D(f) = \alpha \neq k \cdot 90° \, |k \in \mathbb{Z}$
Der Defintionsbereich von Tangens- und Kotangensfunktion ist eingeschränkt, wie du in der Tabelle am Ende des vorigen Kurstextes sehen kannst. Im Gradmaß sind alle ganzzahligen Vielfachen eines rechten Winkels nicht definiert.
Supplementbeziehungen
Supplementbeziehungen (lat. supplementum = Ergänzung) bezeichnen die Beziehungen zweier Winkel, die addiert $180°$ ergeben:
$\alpha + \beta = 180°$
Wir können analog für die Komplementbeziehungen, folgende Gleichungen aufstellen:
$\beta = 180° - \alpha$
Daraus folgt: $\, 180° = \alpha + (180° - \alpha)$
Wir können die Supplementbeziehungen sehr leicht am Verlauf der Sinus- und Kosinuskurven in einem Koordinatensystem herleiten oder am Einheitskreis nachvollziehen:
HIER EIN BILD REIN, WO DER INHALT DER FOLGENDEN GLEICHUNGEN GRAFISCH DARGESTELLT WIRD!!! (Am besten ein 2geteiltes, wo einmal bestimmte Werte für sin und cos und einmal für tan und cot jeweils in einem Koordinatensystem eingezeichnet sind sowie als einfache Variante sin und cos am Einheitskreis dargestellt sind.)
$\, \Longrightarrow sin (\alpha) = sin (180° - \alpha)$
$\, \Longrightarrow - cos (\alpha) = cos (180° - \alpha)$
$\, \Longrightarrow - tan (\alpha) = tan (180° - \alpha)$
$\, \Longrightarrow - cot (\alpha) = cot (180° - \alpha)$
Quadrantenbeziehungen
Komplement- und Supplementbeziehungen gehören zu den sogenannten Quadrantenbeziehungen, mit denen wir die Berechnung jedes beliebigen Winkelfunktionswertes auf die Berechnung eines Winkelfunktionswertes zwischen $0°$ und $90°$ zurückführen können. Du kannst am Einheitskreis wie für die Bestimmung der Supplementbeziehungen in gleicher Weise $\alpha$ von $90°$, $270°$ und $360°$ abziehen oder zu diesen Winkeln addieren.
BEISPIELBILD EINHEITSKREIS: Da dann ein beliebiges alpha zu 90, 180, 270 und 360 Grad addieren und dann die entsprechenden Sinus und Kosinuswerte (ginge auch für tan und cot, reicht aber der Einfachheit halber mit sin und cos farblich hervorheben.
In den folgenden zwei Tabellen haben wir die sogenannten Reduktionsformeln der Quadrantenbeziehungen aufgeführt:
| $90° - \alpha$ | $180° - \alpha$ | $270° - \alpha$ | $360° - \alpha$ | |
| $sin \alpha$ | $+ cos \alpha$ | $+ sin \alpha$ | $- cos \alpha$ | $- sin \alpha$ |
| $cos \alpha$ | $+ sin \alpha$ | $- cos \alpha$ | $- sin \alpha$ | $+ cos \alpha$ |
| $tan \alpha$ | $+ cot \alpha$ | $- tan \alpha$ | $+ cot \alpha$ | $- tan \alpha$ |
| $cot \alpha$ | $+ tan \alpha$ | $- cot \alpha$ | $+ tan \alpha$ | $- cot \alpha$ |
| $90° + \alpha$ | $180° + \alpha$ | $270° + \alpha$ | $360° + \alpha$ | |
| $sin \alpha$ | $+ cos \alpha$ | $- sin \alpha$ | $- cos \alpha$ | $+ sin \alpha$ |
| $cos \alpha$ | $- sin \alpha$ | $- cos \alpha$ | $+ sin \alpha$ | $+ cos \alpha$ |
| $tan \alpha$ | $- cot \alpha$ | $+ tan \alpha$ | $- cot \alpha$ | $+ tan \alpha$ |
| $cot \alpha$ | $- tan \alpha$ | $+ cot \alpha$ | $- tan \alpha$ | $+ cot \alpha$ |
Grundbeziehungen
In Formelsammlungen findest du viele Rechenregeln zum Umrechnen der trigonometrischen Funktionen. Einige Wichtige stellen wir dir kurz vor und benutzen hier die Schreibweise im Bogenmaß, da dieses in den meisten Berechnungen Verwendung findet.
- Eine wichtige Umrechnungsformel ist der trigonometrische Pythagoras.
Merke
Trigonometrischer Pythagoras: $\, sin^2(x) + cos^2(x) = 1, \;\;\; x \in \mathbb{R}$
Teilen wir die Formel des trigonometrischen Pythagoras durch $sin^2(x)$ oder $cos^2(x)$, so erhalten wir:
$\frac{sin^2(x)}{sin^2(x)} + \frac{cos^2(x)}{sin^2(x)} = \frac{1}{sin^2(x)} \;\;\;$ bzw. $\;\;\; \frac{sin^2(x)}{cos^2(x)} + \frac{cos^2(x)}{cos^2(x)} = \frac{1}{cos^2(x)}$
$1 + cot^2(x) = \frac{1}{sin^2(x)} \;\;\;\;\;\;\;\;\;$ bzw. $\;\;\; 1 + tan^2(x) = \frac{1}{cos^2(x)}$
- Da Tangens und Cotangens Umkehrfunktionen voneinander sind, ist ihr Produkt gleich $1$.
Merke
$cot(x) = \frac{1}{tan(x)} \;\; \Longrightarrow \;\; tan(x) \cdot cot(x) = 1, \;\;\; x \in \mathbb{R} \,|x \neq k \cdot \frac{\pi}{2}, k \in \mathbb{Z}$
$ $
- Möchten wir die Summe aus Sinus und Kosinus quadrieren, so wenden wir eine binomische Formel an:
$[sin(x) \pm cos(x)]^2 = sin^2(x) + 2 \, sin(x) \, cos(x) + cos^2(x)$
Aus dem trigonometrischen Pythagoras folgt:
$sin^2(x) + cos^2(x) + 2 \, sin(x) \, cos(x) = 1 + 2 \, sin(x) \, cos(x)$
- Wir setzen in dem Additionstheorem $\, sin(x + y) = sin(x) \, cos(y) + sin(y) \, cos(x) \,$ die beiden Winkel $x$ und $y$ gleich:
$\, x = y \; \longrightarrow \; x + y = 2x \,$
Wir sehen, dass:
$sin(2x) = sin(x) \, cos(x) + sin(x) \, cos(x) = 2 \cdot sin(x) \, cos(x)$
Nun ersetzen wir in der Formel den Term $\, 2 \, sin(x) \, cos(x)$. Für Addition bzw. Subtraktion resultiert die folgende Formel: