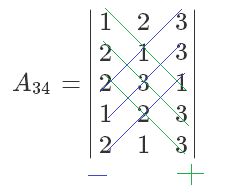Inhaltsverzeichnis
Mit dem Laplaceschen Entwicklungssatz kann man die Determinante einer $(n, n)$ - Matrix „nach einer Zeile oder Spalte entwickeln“.
Merke
Laplaceschen Entwicklungssatz für die i-te Zeile: $A = (a_{ij}) \longrightarrow \; det(A) = \sum\limits_{j = 1}^n (-1)^{i + j} \ a_{ij} \ det (A_{ij})$
Laplaceschen Entwicklungssatz für die j-te Spalte: $A = (a_{ij}) \longrightarrow \; det(A) = \sum\limits_{i = 1}^n (-1)^{i + j} \ a_{ij} \ det (A_{ij})$
Dabei ist $A_{ij}$ die $(n - 1) \times (n - 1)$ - Untermatrix. Sie entsteht durch Streichen der i-ten Zeile und j-ten Spalte. Wie bei der Bestimmung der Determinante vorgegangen wird, zeigen wir dir anhand eines Beispiels.
Entwicklung nach der i-ten Zeile
Beispiel
Gegeben sei die Matrix $A = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \\ 1 & 1 & 3 \end{pmatrix}$. Berechne die Determinante dieser Matrix!
Möchten wir nach der ersten Zeile entwickeln, müssen wir als Erstes die drei Streichungsdeterminanten berechnen, um dann die Determinante von $A$ ermitteln zu können.
Vorgehensweise bei der Entwicklung der 1. Zeile
1. Schritt: Streichen der 1. Zeile und der 1. Spalte:
$A_{11} = \begin{pmatrix} \not{1} & \not{2} & \not{3} \\ \not{2} & 1 & 3 \\ \not{1} & 1 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 3 \\ 1 & 3 \end{pmatrix} \longrightarrow |A_{11}| = \begin{vmatrix} 1 & 3 \\ 1 & 3 \end{vmatrix} = 0$
2. Schritt: Streichen der 1. Zeile und der 2. Spalte:
$A_{12} = \begin{pmatrix} \not{1} & \not{2} & \not{3} \\ 2 & \not{1} & 3 \\ 1 & \not{1} & 3 \end{pmatrix} = \begin{pmatrix} 2 & 3 \\ 1 & 3 \end{pmatrix} \longrightarrow |A_{12}| = \begin{vmatrix} 2 & 3 \\ 1 & 3 \end{vmatrix} = 3$
3. Schritt: Streichen der 1. Zeile und der 3. Spalte:
$A_{13} = \begin{pmatrix} \not{1} & \not{2} & \not{3} \\ 2 & 1 & \not{3} \\ 1 & 1 & \not{3} \end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix} \longrightarrow |A_{13}| = \begin{vmatrix} 2 & 1 \\ 1 & 1 \end{vmatrix} = 1$
4. Schritt: Einsetzen in die Formel:
$det(A) = \sum\limits_{j = 1}^n (-1)^{1 + j} \cdot a_{1j} \cdot det (A_{1j})$
$= (-1)^{1 + 1} \cdot 1 \cdot 0 + (-1)^{1 + 2} \cdot 2 \cdot 3 + (-1)^{1 + 3} \cdot 3 \cdot 1 = -3$
Die Determinante von $A$ beträgt demnach $-3$.
Entwicklung nach der j-ten Spalte
Beispiel
Gegeben sei dieselbe Matrix $A = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \\ 1 & 1 & 3 \end{pmatrix}$. Berechne die Determinante dieser Matrix!
Möchten wir nach der ersten Spalte entwickeln, müssen wir wieder zunächst die drei Streichungsdeterminanten berechnen, um dann die Determinante von $A$ ermitteln zu können.
Vorgehensweise bei der Entwicklung der 1. Spalte
1. Schritt: Streichen der 1. Spalte und der 1. Zeile:
$A_{11} = \begin{pmatrix} \not{1} & \not{2} & \not{3} \\ \not{2} & 1 & 3 \\ \not{1} & 1 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 3 \\ 1 & 3 \end{pmatrix} \longrightarrow |A_{11}| = \begin{vmatrix} 1 & 3 \\ 1 & 3 \end{vmatrix} = 0$
2. Schritt: Streichen der 1. Spalte und der 2. Zeile:
$A_{21} = \begin{pmatrix} \not{1} & 2 & 3 \\ \not{2} & \not{1} & \not{3} \\ \not{1} & 1 & 3 \end{pmatrix} = \begin{pmatrix} 2 & 3 \\ 1 & 3 \end{pmatrix} \longrightarrow |A_{21}| = \begin{vmatrix} 2 & 3 \\ 1 & 3 \end{vmatrix} = 3$
3. Schritt: Streichen der 1. Spalte und der 3. Zeile:
$A_{31} = \begin{pmatrix} \not{1} & 2 & 3 \\ \not{2} & 1 & 3 \\ \not{1} & \not{1} & \not{3} \end{pmatrix} = \begin{pmatrix} 2 & 3 \\ 1 & 3 \end{pmatrix} \longrightarrow |A_{31}| = \begin{vmatrix} 2 & 3 \\ 1 & 3 \end{vmatrix} = 3$
4. Schritt: Einsetzen in die Formel:
$det(A) = \sum\limits_{i = 1}^n (-1)^{i + 1} \cdot a_{i1} \cdot det (A_{i1})$
$= (-1)^{1 + 1} \cdot 1 \cdot 0 + (-1)^{2 + 1} \cdot 2 \cdot 3 + (-1)^{3 + 1} \cdot 1 \cdot 3 = -3$
Die Determinante von $A$ beträgt demnach $-3$.
Anwendungsbeispiel
Beispiel
Gegeben sei die Matrix $A = \begin{pmatrix} 1 & 2 & 3 & 0 \\ 2 & 1 & 3 & 0\\ 1 & 1 & 3 & 1 \\ 2 & 3 & 1 & 0 \end{pmatrix}$. Berechne die Determinante von $A$!
Wir entwickeln nach der 4. Spalte, da in dieser die meisten Nullen stehen und sich die Determinante damit einfacher berechnen lässt.
1. Schritt: Streiche 4. Spalte und 1. Zeile:
$|A_{14}| = \begin{vmatrix} \not1 & \not2 & \not3 & \not0 \\ 2 & 1 & 3 & \not0\\ 1 & 1 & 3 & \not1 \\ 2 & 3 & 1 & \not0 \end{vmatrix} = \begin{vmatrix} 2 & 1 & 3 \\ 1 & 1 & 3 \\ 2 & 3 & 1 \end{vmatrix}$
Die Determinante muss hier nicht berechnet werden, da das Element der Matrix in der Laplaceschen Entwicklungsformel $a_{14} = 0$. Damit wird der gesamte Term
$(-1)^{1 + 4} \cdot a_{14} \cdot det(A_{14}) = 0$.
Das Gleiche gilt für $|A_{24}|$ und $|A_{44}|$.
Für $|A_{34}|$ allerdings ist das Element $a_{34} = 1$. Demnach wird der Term
$(-1)^{3 + 4} \cdot a_{34} \cdot det(A_{34}) \neq 0$,
weshalb wir die Streichungsdeterminante $det(A_{34})$ bestimmen müssen.
2. Schritt: Streiche 4. Spalte und 3. Zeile:
$|A_{34}| = \begin{vmatrix} 1 & 2 & 3 & \not0 \\ 2 & 1 & 3 & \not0\\ \not1 & \not1 & \not3 & \not1 \\ 2 & 3 & 1 & \not0 \end{vmatrix} = \begin{vmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \\ 2 & 3 & 1 \end{vmatrix}$
3. Schritt: Anwendung der Regel von Sarrus:
$det(A_{34}) = 1 \cdot 1 \cdot 1 + 2 \cdot 3 \cdot 3 + 2 \cdot 2 \cdot 3 - 3 \cdot 1 \cdot 2 - 3 \cdot 3 \cdot 1 - 1 \cdot 2 \cdot 2 = 12$
4. Schritt: Einsetzen in die Formel:
$det(A) = (-1)^{3 + 4} \cdot a_{34} \cdot det (A_{34}) = (-1)^{3 + 4} \cdot 1 \cdot 12 = -12$
Die Determinante von $A$ beträgt demnach $-12$.
Regeln für Elementare Umformungen
Für größere Matrizen empfiehlt sich die Matrix in eine einfachere Form zu bringen. Allerdings haben elementare Umformungen von Matrizen Auswirkungen auf die Determinante. Im Folgenden haben wir diese Auswirkungen für dich zusammengefasst.
Merke
Folgenden Regeln bei der Umformung von Matrizen sollten bekannt sein und können dadurch eine Berechnung vereinfachen:
- Die Determinante einer Diagonalmatrix ist das Produkt der Hauptdiagonalelemente.
- Die Determinante ist linear in jeder Spalte.
- Das Tauschen von 2 Spalten führt zum Vorzeichenwechsel der Determinanten.
- Die Determinante einer Matrix mit linear abhängigen Spalten ist stets gleich Null.
- Die Determinante ändert sich nicht, wenn man ein Vielfaches einer Zeile oder Spalte zu einer anderen addiert.
- Eine Matrix ist nur dann invertierbar, wenn ihre Determinante ungleich Null ist.
Weitere interessante Inhalte zum Thema
-
Rang einer Matrix
Vielleicht ist für Sie auch das Thema Rang einer Matrix (Matrizen) aus unserem Online-Kurs Analysis und Lineare Algebra interessant.