Inhaltsverzeichnis
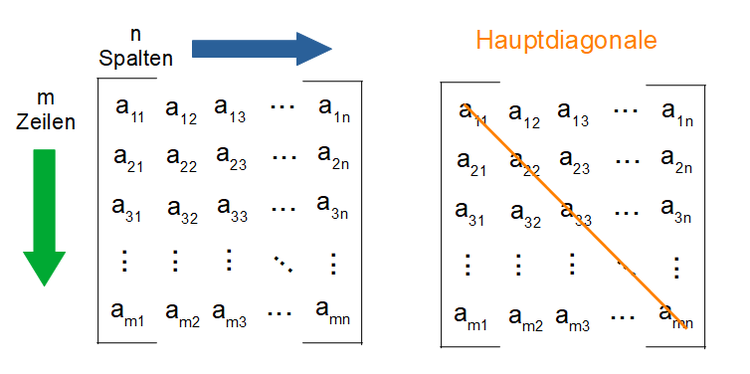
Eine Matrix ist ein rechteckiges Zahlenschema, welche aus $m \times n$ Zahlen (Elementen) besteht. Diese sind in $m$-Zeilen (Zeilenvektoren) und $n$-Spalten (Spaltenvektoren) angeordnet. Die allgemeine Form einer Matrix ist:
Es gibt unterschiedliche Erscheinungsformen einer Matrix, die wir uns im Nachfolgenden mal genauer anschauen wollen.
Einheitsmatrix
Für die Einheitsmatrix gilt, dass die Elemente $a_{mn}$ auf der Diagonalen den Wert 1 annehmen, wobei alle übrigen Elemente den Wert Null annehmen.
$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$
Die obige Matrix ist eine $3 \times 3$ Matrix. Alle Elemente auf der Hauptdiagonalen nehmen den Wert 1 an, alle übrigen Elemente sind Null.
Hinweis
Es existiert für jede Größe einer Matrix eine zugehörige Einheitsmatrix!
Matrix (m-Spalten, n-Zeilen)
Es gibt Matrizen, bei denen die Zeilen- und Spaltenanzahl unterschiedlich ist, wie in den nachfolgenden beiden Beispielen dargestellt:
$A = \begin{pmatrix} 2 & 7 \\ 1 & 3\\ 2 & 4 \end{pmatrix}$
$A = \begin{pmatrix} 3 & -7 & 2 \end{pmatrix}$
Quadratische Matrix
Eine quadratische Matrix ist - wie der Name bereits aussagt - eine Matrix, die eine quadratische Form aufweist. Hier ist die Anzahl der Zeilen und Spalten identisch.
$A = \begin{pmatrix} 1 & 8 \\ 3 & -2 \end{pmatrix}$
$A = \begin{pmatrix} 2 & 7 & 4 \\ 1 & 3 & 2 \\ 2 & 4 & 7 \end{pmatrix}$
$A = \begin{pmatrix} 2 & 7 & 4 & -2 \\ 1 & -4 & 2 & 5 \\ 1 & 6 & 7 & 9 \\ -7 & 4 & 2 & 1 \end{pmatrix}$
Nullmatrix
Von einer Nullmatrix ist die Rede, wenn alle Elemente innerhalb der Matrix den Wert Null annehmen.
$A = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$
Transponierte Matrix
Vertauscht man in einer Matrix die Zeilen mit den entsprechenden Spalten, so entsteht eine transponierte Matrix $\ A^T$ (oder Schreibweise $A'$):
$A = (a_{ik})_{m,n} \longleftrightarrow A^T = (a_{ki})_{n,m}$
Hinweis
In Worten: Beim transponieren wird die 1. Zeile mit der 1. Spalte, die 2. Zeile mit der 2. Spalte usw. getauscht.
Dazu betrachen wir das nachfolgende Beispiel:
Beispiel
$A_{3,4} = \begin{pmatrix} 7 & 4 & 3 & 5 \\ 1 & 0 & 7 & 6 \\ 4 & 2 & 9 & 8 \end{pmatrix} \longleftrightarrow A^T = \begin{pmatrix} 7 & 1 & 4 \\ 4 & 0 & 2 \\ 3 & 7 & 9 \\ 5 & 6 & 8 \end{pmatrix}$
Die folgenden Regeln beim Transponieren einer Matrix müssen beachtet werden:
- $\ (A^T)^T = A $
- $\ (A + B)^T = A^T + B^T $
- $\ (sA)^T = s \cdot A^T \;\;\;$ ($s$ ist ein Skalar.)
- $\ (AB)^T = B^T \cdot A^T $
Symmetrische Matrix
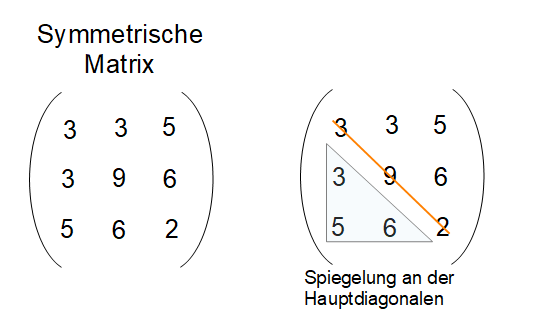
Eine symmetrische Matrix ist eine quadratische Matrix (siehe oben), bei welcher die Einträge spiegelsymmetrisch bezüglich der Hauptdiagonalen sind. Eine symmetrische Matrix stimmt mit ihrer transponierten Matrix überein.
Weitere interessante Inhalte zum Thema
-
Eigenvektoren
Vielleicht ist für Sie auch das Thema Eigenvektoren (Matrizen) aus unserem Online-Kurs Analysis und Lineare Algebra interessant.