Inhaltsverzeichnis
Die Addition von zwei Vektoren $\vec{a} = \left(\begin{array}{c} x_1 \\ y_1 \end{array} \right)$ und $\vec{b} = \left(\begin{array}{c} x_2 \\ y_2 \end{array} \right)$ ist definiert durch:
$\vec{a} + \vec{b} := \left( \begin{array}{c} x_1 + x_2 \\ y_1 + y_2 \end{array} \right)$
Die grafische Addition von Vektoren erfolgt, indem der Anfangspunkt des Vektors $\vec{b}$ an den Endpunkt des Vektors $\vec{a}$ angreiht wird. Dabei darf die Richtung der Vektoren nicht verändert werden. Der resultierende Vektor $\vec{a} + \vec{b}$ wird dann bestimmt, indem der Anfangspunkt des resultierenden Vektors an den Anfangspunkt des ersten Vektors gelegt wird und die Spitze des resultierenden Vektors an die Spitze des letzten Vektors.
Beispiel
Gegeben sei der Vektor $\vec{a} = (1,2)$ und der Vektor $\vec{b} = (-5,3)$.
Führe bitte die Addition der beiden Vektoren durch und veranschauliche dies grafisch!
Die Addition wird wie folgt durchgeführt:
$\vec{a} + \vec{b} = (1-5, 2+3) = (-4,5)$
Dieser resultierende Vektor ist ein Ortsvektor, welcher im Ursprung beginnt (so wie auch die Vektoren $\vec{a}$ und $\vec{b}$) und auf den Punkt $(-4,5)$ zeigen.
Grafisch sieht das Ganze wie folgt aus.
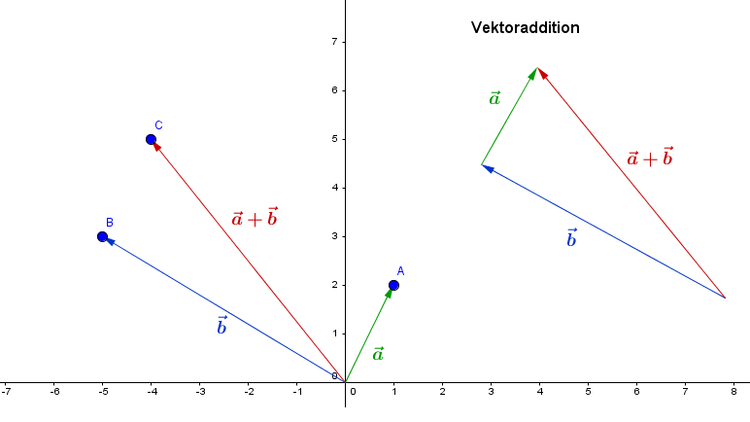
In der obigen Grafik sind unten links die Ortsvektoren $\vec{a}$ und $\vec{b}$ und die Summe aus diesen beiden $\vec{a} + \vec{b}$ zu sehen. Diese beginnen im Ursprung $(0,0)$ und zeigen auf die Punkte $A$, $B$ und $C$.
Bei der grafischen Addition (oben rechts) wird wie folgt vorgegangen:
Der Anfangspunkt des Vektors $\vec{b}$ wird an den Endpunkt von Vektor $\vec{a}$ gelegt bzw. der Anfangspunkt von Vektor $\vec{a}$ an den Endpunkt von Vektor $\vec{b}$ (Kommutativgesetz). Das Ergebnis dieser grafischen Addition ist der neue Vektor $\vec{a} + \vec{b}$. Dieser wird bestimmt, indem der Anfangspunkt des 1. Vektors und der Endpunkt des letzten Vektors miteinander verbunden werden. Dabei zeigt die Spitze des neuen Vektors auf die Spitze des letzten Vektors.
Im Folgenden zeigen wir dir die Rechenregeln für die Addition von Vektoren.
Kommutativgesetz
Das Kommutativgesetz besagt, dass Argumente (Vektoren) einer Operation (Addition) vertauscht werden können, ohne dass sich am Ergebnis etwas ändert:
Methode
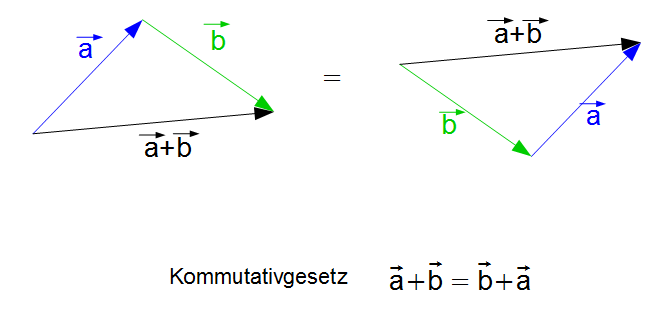
Kommutativgesetz: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$
In der folgenden Grafik ist das Kommutativgesetz veranschaulicht.
Assoziativgesetz
Das Assoziativgesetz besagt, dass man Summanden beliebig zusammenfassen darf, die Summe bleibt immer gleich. Die allgemeine Schreibweise sieht wie folgt aus:
Methode
Assoziativgesetz: $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) = \vec{a} + \vec{b} + \vec{c}$
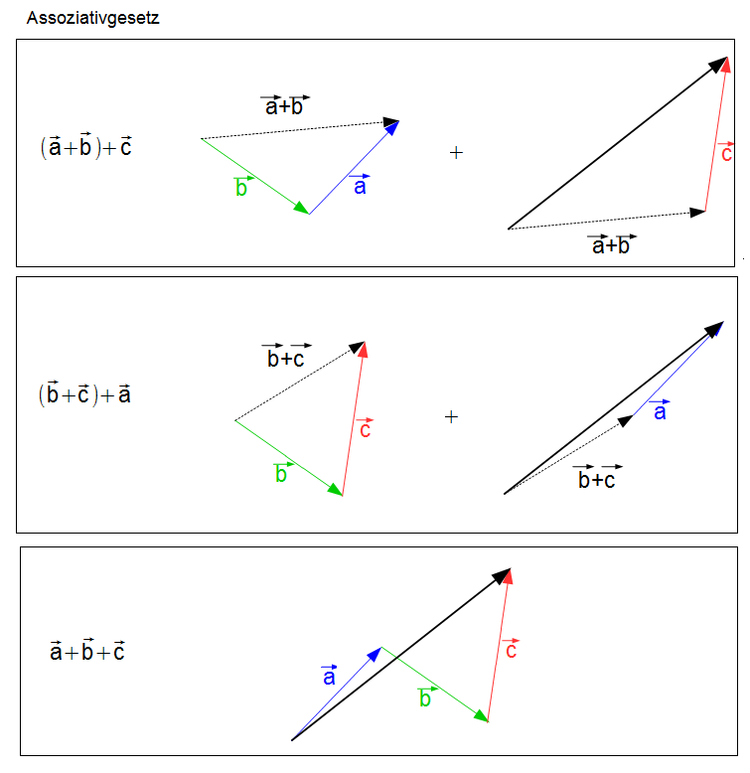
In der folgenden Grafik ist das Assoziativgesetz für die drei Vektoren $\vec{a}$, $\vec{b}$ und $\vec{c}$ veranschaulicht.
Der resultierende Vektor (dicker schwarzer Vektor) ist bei allen drei Operationen identisch.
Nullvektor
Ein Nullvektor ergibt sich, wenn der Anfangspunkt des ersten Vektors mit dem Endpunkt des letzten Vektors zusammenfällt.
$\vec{0} = \vec{a} + \vec{b} + \vec{c} + ... + \vec{n}$
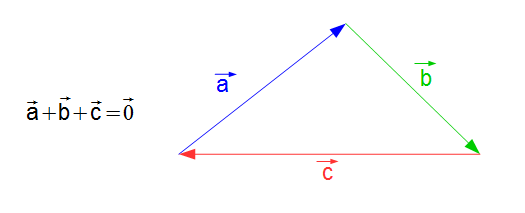
Die beispielhafte Skizze der Vektoren $\vec{a} + \vec{b} + \vec{c} = \vec{0}$ sieht folgendermaßen aus:
In der obigen Grafik ist deutlich zu erkennen, dass der Anfangspunkt des ersten Vektors mit dem Endpunkt des letzten Vektors zusammenfällt. Das bedeutet, dass hier kein resultierender Vektor existiert und demnach das Ergebnis ein Nullvektor ist.
Anwendungsbeipiel: Kommutativgesetz
Beispiel
Der Summenvektor ist:
$\vec{a} + \vec{b} = (12, 8)$
$\vec{b} + \vec{a} = (12,8)$
Anwendungsbeispiel: Assoziativgesetz
Beispiel
Assoziativgesetz:
(1) $(\vec{a} + \vec{b}) = (12,8)$
$(\vec{a} + \vec{b}) + \vec{c} = (13,11)$
(2) $(\vec{b} + \vec{c}) = (9,5)$
$(\vec{b} + \vec{c}) + \vec{a} = (13,11)$