Merke
Die Subtraktion von zwei Vektoren $\vec{a} = \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right)$ und $\vec{b} = \left( \begin{array}{c} x_2 \\ y_2 \end{array} \right)$ ist definiert durch:
$\vec{a} - \vec{b} := \left( \begin{array}{c} x_1 - x_2 \\ y_1 - y_2 \end{array} \right)$
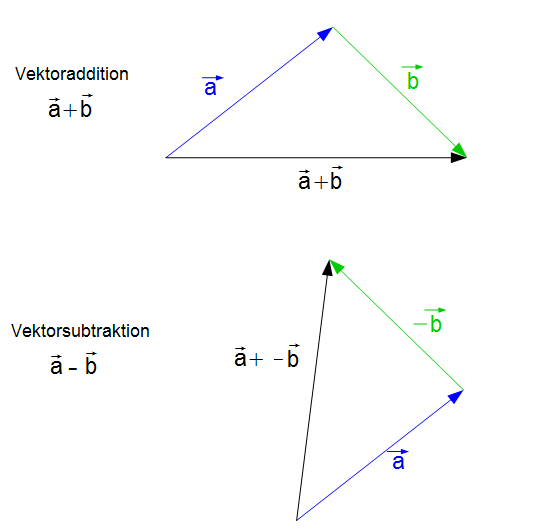
Die grafische Subtraktion des Vektors $\vec{b}$ vom Vektor $\vec{a}$ erfolgt, indem man den entgegengesetzten Vektor $- \vec{b}$ zum Vektor $\vec{a}$ hinzuaddiert. Man tauscht also zunächst den Anfangspunkt und Endpunkt des Vektors $\vec{b}$ miteinander. Man hat denn den Vektor $-\vec{b}$ gegeben.
Dann legt man (wie bei der Vektoraddition) den Anfangspunkt des Vektors $-\vec{b}$ an den Endpunkt des Vektors $\vec{a}$. Der resultierende Vektor $\vec{a} - \vec{b}$ wird dann bestimmt, indem der Anfangspunkt des resultierenden Vektors an den Anfangspunkt des ersten Vektors gelegt wird und die Spitze des resultierenden Vektors an die Spitze des letzten Vektors.
In der folgenden Grafik ist die grafische Addition und Subtraktion von Vektoren gegenübergestellt:
Beispiel
a) $\vec{a} + \vec{b} + \vec{c}$
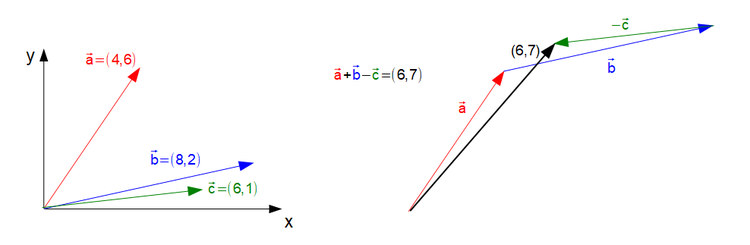
b) $\vec{a} + \vec{b} - \vec{c}$
c) $\vec{a} - \vec{b} - \vec{c}$
a) $\vec{a} + \vec{b} + \vec{c} = (18, 9)$
b) $\vec{a} + \vec{b} - \vec{c} = (6,7)$
c) $\vec{a} - \vec{b} - \vec{c} = (-10, 3)$
Der Aufgabenteil b) sieht dann grafisch wie folgt aus: