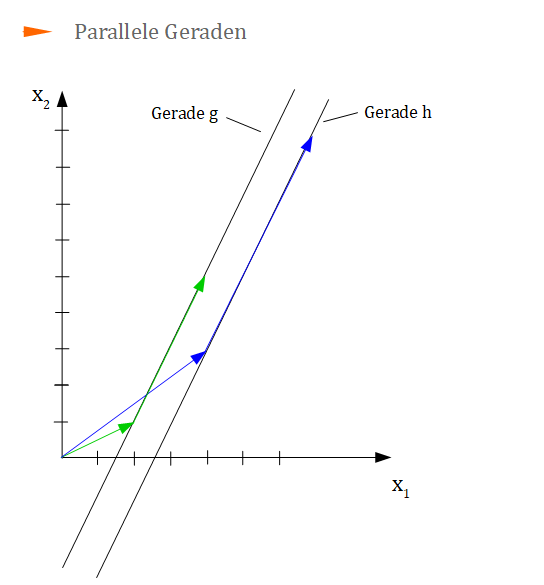
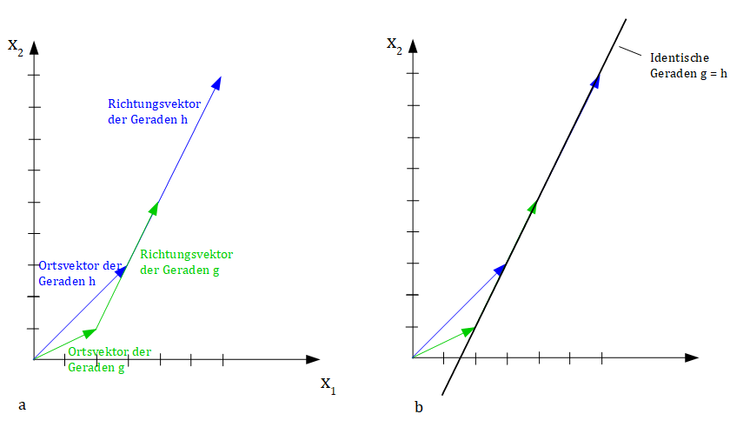
Wir haben bereits identische Geraden kennengelernt. Parallele Geraden liegen - wie der Name bereits vermuten lässt - parallel zueinander. Zwei Geraden sind genau dann parallel, wenn sie in jedem Punkt denselben Abstand haben.
Für die Überprüfung muss die erste Bedingung der identischen Geraden erfüllt sein, deren zweite Bedingung darf jedoch nicht erfüllt sein.
Bedingungen für parallele Geraden:
Methode
1. Die Richtungsvektoren der Geraden sind Vielfache voneinander.
2. Der Aufpunkt der einen Geraden befindet sich nicht auf der anderen Geraden.
Sind diese Bedingung erfüllt, so handelt es sich um parallele Geraden.
Beispiel 1: Parallele Geraden in der Ebene
Beispiel
Gegeben seien die beiden Geraden:
$g: \vec{x} = \left(\begin{array}{c} 2 \\ 1 \end{array}\right) + t_1 \cdot \left(\begin{array}{c} 2 \\ 4 \end{array}\right) $
$h: \vec{x} = \left(\begin{array}{c} 4 \\ 3 \end{array}\right) + t_2 \cdot \left(\begin{array}{c} 3 \\ 6 \end{array}\right) $
Prüfe, ob die beiden Geraden parallel zueinander sind!
Zunächst betrachten wir die beiden Richtungsvektoren:
$\left(\begin{array}{c} 2 \\ 4 \end{array}\right) = \lambda \left(\begin{array}{c} 3 \\ 6 \end{array}\right)$
Wir stellen das lineare Gleichungssystem auf:
(1) $2 = 3 \lambda$
(2) $4 = 6 \lambda$
Nach $\lambda$ auflösen:
(1) $\lambda = \frac{2}{3}$
(2) $\lambda = \frac{2}{3}$
$\lambda$ ist in beiden Zeilen gleich, d. h. die Richtungsvektoren sind Vielfache voneinander. Die 1. Bedingung ist erfüllt. Damit es sich um parallele Geraden handelt und nicht um identische, darf der Aufpunkt der einen Geraden nicht auf der anderen Geraden liegen. Wir setzen dazu den Aufpunkt der Geraden $g$ mit der Geradengleichung $h$ gleich:
$\left(\begin{array}{c} 2 \\ 1 \end{array}\right) = \left(\begin{array}{c} 4 \\ 3 \end{array}\right) + t_2 \cdot \left(\begin{array}{c} 3 \\ 6 \end{array}\right) $
Aufstellung des linearen Gleichungssystems:
(1) $2 = 4 + 3 t_2$
(2) $1 = 3 + 6 t_2$
Auflösen nach $t_2$:
(1) $t_2 = -\frac{2}{3}$
(2) $t_2 = - \frac{1}{3}$
Da in den beiden Zeilen die Werte für $t_2$ nicht identisch sind, liegt der Aufpunkt der Geraden $g$ nicht auf der Geraden $h$. Damit liegen hier parallele Geraden vor.
Beispiel 2: Parallele Geraden im Raum
Beispiel
Gegeben seien die beiden Geraden:
$g: \vec{x} = \left(\begin{array}{c} 4 \\ 2 \\ -4 \end{array}\right) + t_1 \cdot \left(\begin{array}{c} 8 \\ -4 \\ 2 \end{array}\right) $
$h: \vec{x} = \left(\begin{array}{c} -3 \\ 4 \\ -5 \end{array}\right) + t_2 \cdot \left(\begin{array}{c} -2 \\ 1 \\ -0,5 \end{array}\right) $
Prüfe, ob die beiden Geraden parallel sind!
Zunächst prüfen wir ob die beiden Richtungsvektoren Vielfache voneinander sind:
$\left(\begin{array}{c} 8 \\ -4 \\ 2 \end{array}\right) = \lambda \left(\begin{array}{c} -2 \\ 1 \\ -0,5 \end{array}\right) $
Wir stellen das Gleichungssystem auf:
(1) $ 8 = -2 \lambda$
(2) $ -4 = 1 \lambda$
(3) $2 = -0,5 \lambda$
Auflösen nach $\lambda$:
(1) $\lambda = -4$
(2) $\lambda = -4$
(3) $\lambda = -4$
$\lambda$ ist in allen Zeilen identisch, damit sind die Richtungsvektoren der beiden Geraden Vielfache voneinander.
Um identische Geraden ausschließen zu können, darf der Aufpunkt der einen Geraden nicht auf der anderen Geraden liegen. Wir setzen dazu den Aufpunkt der Geraden $g$ mit der Geradengleichung $h$ gleich:
$\left(\begin{array}{c} 4 \\ 2 \\ -4 \end{array}\right) = \left(\begin{array}{c} -3 \\ 4 \\ -5 \end{array}\right) + t_2 \cdot \left(\begin{array}{c} -2 \\ 1 \\ -0,5 \end{array}\right) $
Wir stellen das Gleichungssystem auf:
(1) $4 = -3 - 2 t_2$
(2) $2 = 4 + t_2$
(3) $-4 = -5 - 0,5 t_2$
Wir lösen nach $t_2$ auf:
(1) $t_2 = - 3,5$
(2) $t_2 = -2$
(3) $t_2 = -2$
Die Werte sind für $t_2$ nicht identisch, d. h. der Aufpunkt der Geraden $g$ liegt nicht auf der Geraden $h$. Damit liegen diese Geraden parallel zueinander.
Weitere interessante Inhalte zum Thema
-
Identische Geraden
Vielleicht ist für Sie auch das Thema Identische Geraden (Vektorrechnung) aus unserem Online-Kurs Analysis und Lineare Algebra interessant.