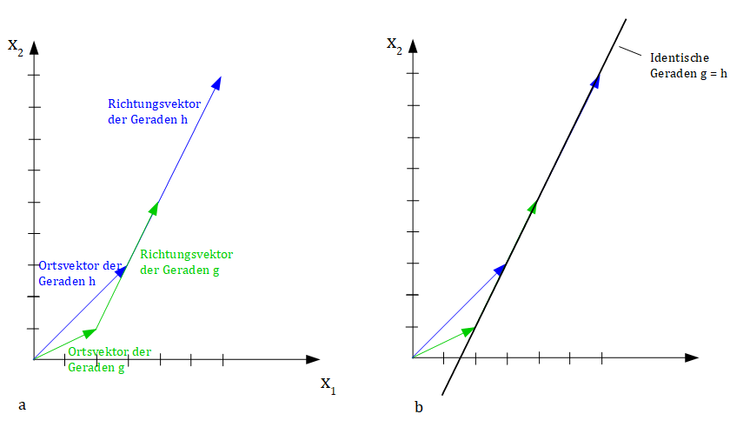
Geraden werden als windschief bezeichnet, wenn sie sich weder schneiden noch parallel zueinander sind. Im zweidimensionalen Raum sind zwei Geraden entweder parallel zueinander (bzw. identisch) oder schneiden sich. Windschiefe Geraden können also nur in mindestens dreidimensionalen Räumen auftreten.
Die Voraussetzungen für windschiefe Geraden sind:
Methode
- Die Richtungsvektoren der Geraden sind nicht Vielfache voneinander.
- Die Geraden schneiden sich nicht.
Zum besseren Verständnis folgt ein Beispiel zum Nachweis von windschiefen Geraden.
Beispiel: Windschiefe Geraden
Beispiel
Gegeben seien die beiden Geraden:
$g : \vec{x} = \left(\begin{array}{c} 2 \\ -1 \\ 3 \end{array}\right) + t_1 \cdot \left(\begin{array}{c} 0 \\ -2 \\ 1 \end{array}\right) $
$h : \vec{x} = \left(\begin{array}{c} 1 \\ 0 \\ -2 \end{array}\right) + t_2 \cdot \left(\begin{array}{c} -1 \\ 1 \\ 2 \end{array}\right) $
Zeige, dass die beiden Geraden windschief zueinander sind!
Wir müssen zunächst zeigen, dass die beiden Geraden nicht linear abhängig voneinander sind.
Dazu betrachten wir die beiden Richtungsvektoren:
$\left(\begin{array}{c} 0 \\ -2 \\ 1 \end{array}\right) = \lambda \left(\begin{array}{c} -1 \\ 1 \\ 2 \end{array}\right) $
Wir stellen das lineare Gleichungssystem auf:
(1) $0 = - \lambda$
(2) $-2 = \lambda$
(3) $1 = 2 \lambda$
Sind alle $\lambda$ gleich, so handelt es sich um linear abhängige Vektoren und damit sind diese parallel (oder sogar identisch).
(1) $\lambda = 0$
(2) $\lambda = -2$
(3) $\lambda = \frac{1}{2}$
Die Vektoren sind linear voneinander unabhängig, weil in den Zeilen nicht immer derselbe Wert für $\lambda$ resultiert.
Die beiden Geraden sind demnach nicht parallel. Entweder schneiden sie sich in einem Punkt oder sie sind windschief zueinander.
Wir prüfen, ob ein Schnittpunkt vorliegt, indem wir beiden Geraden gleich setzen:
$\left(\begin{array}{c} 2 \\ -1 \\ 3 \end{array}\right) + t_1 \cdot \left(\begin{array}{c} 0 \\ -2 \\ 1 \end{array}\right) = \left(\begin{array}{c} 1 \\ 0 \\ -2 \end{array}\right) + t_2 \cdot \left(\begin{array}{c} -1 \\ 1 \\ 2 \end{array}\right) $
Wir stellen das lineare Gleichungssystem auf:
(1) $2 + 0 t_1 = 1 - t_2$
(2) $-1 -2 t_1 = 0 + t_2$
(3) $3 + t_1 = -2 + 2 t_2$
Aus (1) kann sofort $t_2$ bestimmt werden:
(1) $t_2 = -1$
Einsetzen in (2):
(2) $-1 -2 t_1 = 0 + (-1)$
$2t_1 = 0$
$t_1 = 0$
Damit die Geraden nun einen Schnittpunkt haben, muss die Gleichung (3) eine Lösung haben. Zur Überprüfung setzen wir die Ergebnisse in die Gleichung (3) ein:
(3) $3 +0 = -2 + 2 \cdot (-1)$
$3 = -4$
Diese Aussage ist falsch, damit besitzen die beiden Geraden keinen Schnittpunkt. Damit sind $g$ und $h$ windschief zueinander!
Weitere interessante Inhalte zum Thema
-
Identische Geraden
Vielleicht ist für Sie auch das Thema Identische Geraden (Vektorrechnung) aus unserem Online-Kurs Analysis und Lineare Algebra interessant.
-
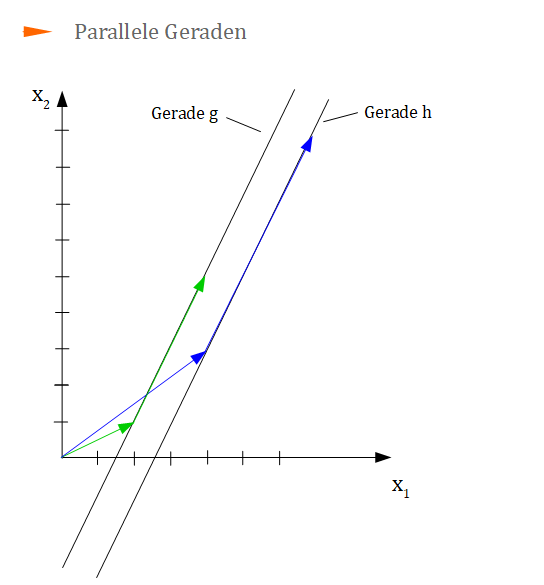
Parallele Geraden
Vielleicht ist für Sie auch das Thema Parallele Geraden (Vektorrechnung) aus unserem Online-Kurs Analysis und Lineare Algebra interessant.