Inhaltsverzeichnis
Beispiel
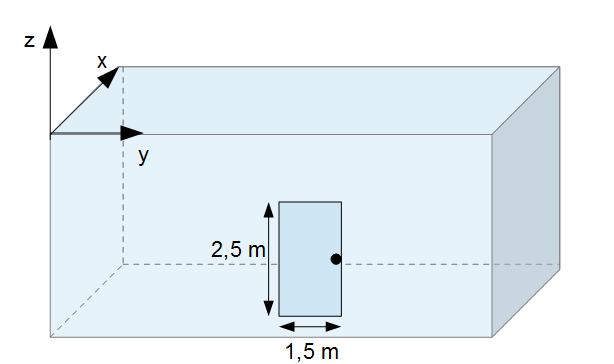
Gegeben sei ein Wasserbecken. Das Wasserbecken besteht aus Betonwänden. In einer dieser Wände befindet sich eine Tür. Diese Tür hat eine Höhe von 2,5 m, eine Länge von 1,5 m und eine Breite (Tiefe) von 1 m. Insgesamt ergeben sich 3,75 m³. Der Schwerpunkt der Tür befindet sich in 5 m Tiefe. Es soll die Horizontalkraft und die Vertikalkraft bestimmt werden. Außerdem die Resultierende und ihre Wirkungslinie.
Berechnung der Horizontalkraft
In diesem Beispiel wirkt nur eine Horizontalkraft ($x$-Richtung) auf die Tür. Eine Vertikalkraft ($z$-Richtung) existiert hier nicht (zumindest nicht durch das Wasser). Es muss also die Horizontalkraft bestimmt werden:
$F_H = p_s \cdot A_{proj}$
$F_H = \rho \; g \; h_s \cdot A_{proj}$.
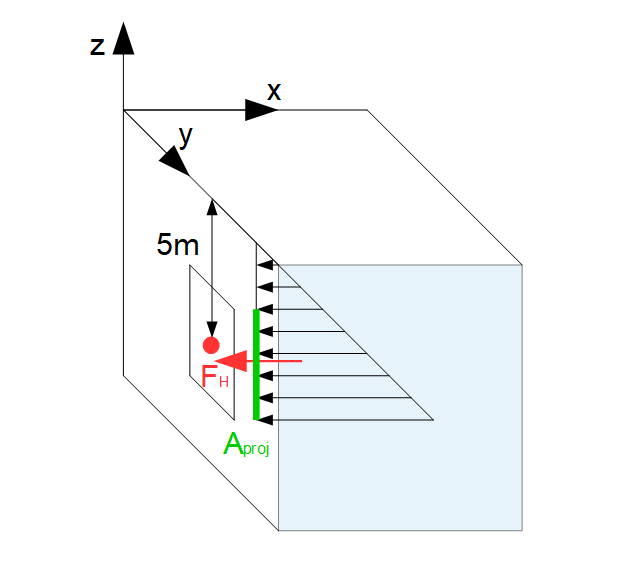
Für die Berechnung muss zunächst wieder eine Fläche projiziert werden:
In der obigen Grafik ist nun der Schwerpunkt (rot) der Tür eingezeichnet. Der Schwerpunkt befindet sich in der Mitte der Tür (rechteckige Fläche). Der schwarze Türknauf wurde der Übersicht halber entfernt. Der Schwerpunkt befindet sich 5 m tief unter Wasser.
Die Horizontalkraft wird bestimmt durch:
$F_H = \rho \; g \; h_s \cdot A_{proj}$.
$h_s$ ist dabei der senkrechte Abstand des Schwerpunktes zur Flüssigkeitsoberfläche. Dieser ist bereits in der Aufgabenstellung gegeben: $h_s = 5m$.
$F_H = 999,97 \frac{kg}{m^3} \cdot 9,81 \frac{m}{s^2} \cdot 5 m \cdot A_{proj}$.
Da wir nur die Druckkraft auf die Tür benötigen, muss auch nur die Türfläche projiziert werden. Da sich die Tür in einer senkrechten Wand befindet, ist die projizerte Fläche und die Fläche der Tür identisch. Es handelt sich um eine rechteckige Fläche, demach ergibt sich der Flächeninhalt aus Höhe mal Breite: $A_{proj} = A_{Tür} = 2,5m \cdot 1,5m = 3,75m^2$.
Merke
Sollte die Breite $y = b$ in der Aufgabenstellung nicht angegeben sein, dann geht man immer von 1 m aus!
Merke
Um den Flächeninhalt der projizierten Fläche zu bestimmen und hier auch die richtigen Werte zu verwenden, kann man sich folgendes merken: Wenn man die Horizontalkraft in $x$-Richtung bestimmt, dann ergibt sich die projizierte Fläche (m²) aus den Abmessungen in $y$-Richtung und in $z$-Richtung.
Für die Tür bedeutet dies, dass für die projizierte Fläche die Abmessungen in $y$-Richtung, also 1,5 m und die Abmessungen in $z$-Richtung, also 2,5 m, benötigt werden.
$F_H = 999,97 \frac{kg}{m^3} \cdot 9,81 \frac{m}{s^2} \cdot 5 m \cdot 3,75 m^2$.
$F_H = 183.931,98 N = 183,93 kN$.
Resultierende und Wirkungslinie
Wir haben eine vertikale Wand gegeben. Demnach ist die resultierende Druckkraft $F_R$ gleich der horizontalen Durckkraft $F_H$:
$F_R = \sqrt{F_V^2 + F_H^2} = \sqrt{F_H^2} = \sqrt{ 183,93^2 kN^2} = 183,93 kN$.
Da keine Vertikalkraft existiert, ist die Resultierende gleich der Horizontalkraft.
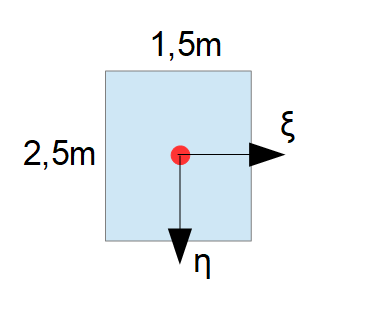
Wir wollen als nächstes herausfinden, in welchem Punkt die Resultierende angreift (=Durckmittelpunkt). Um nun den Druckmittelpunkt bestimmen zu können, wird ein $\eta, \xi$-Koordinatensystem eingeführt, welches genau durch den Schwerpunkt der Fläche verläuft:
Die $\eta$-Achse wird dabei in Richtung der Wand gelegt, in welcher sich die Tür befindet. In diesem Fall also eine senkrechte Wand und damit eine senkrechte $\eta$-Achse.
Es kann nun mittels der folgenden Gleichungen der Abstand des Druckmittelpunktes zum Schwerpunkt in Richtung der $\eta$-Achse bestimmt werden:
Methode
$\eta_D = \frac{I_{\xi,S}}{\eta_S \; A}$.
$\eta_D$ liefert den Abstand vom Schwerpunkt zum Druckmittelpunkt hin.
Flächenträgheitsmoment $I_{\xi,S}$ für Rechteck ist Tabellenwerken zu entnehmen:
$I_{\xi,S} = \frac{(2,5m)^3 \cdot 1,5 m}{12} = 1,95m^4$.
$\eta_S$ ist der Abstand vom Schwerpunkt zur Flüssigkeitsoberfläche in $\eta$-Richtung:
$\eta_S = 5 m$.
Fläche ist:
$A = 1,5 m \cdot 2,5 m = 3,75 m^2$.
Insgesamt ergibt sich:
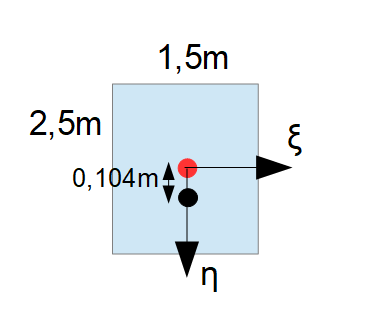
$\eta_D = \frac{1,95m^4}{5m \cdot 3,75m^2} = 0,104 m$.
Hierbei handelt es sich um den Abstand vom Schwerpunkt zum Druckmittelpunkt in $\eta$-Richtung. Der gesamte Abstand von der Flüssigkeitsoberfläche zum Druckmittelpunkt in $\eta$-Richtung beträgt dann:
$0,104 m + 5m = 5,104 m$.
Der Abstand in $\xi$-Richtung vom Schwerpunkt zum Druckmittelpunkt wird berechnet mit:
Methode
$\xi_D = \frac{I_{\eta \xi}}{\eta_S \; A}$
$\xi_D$ liefert den Abstand vom Schwerpunkt zum Druckmittelpunkt hin.
Die $\xi$-Achse stellt eine Symmetrieachse dar. Das bedeutet, dass hier das Deviationsmoment (auch: Zentrifugalmoment) null wird:
$I_{\eta \xi} = 0$.
Insgesamt wird also der gesamte Term null:
$\xi_D = 0$.
Die Wirkungslinie der Horizontalkraft $F_H$ liegt also bei 5,104 m Tiefe.
Beispiel: Druck auf den Behälterboden
Beispiel
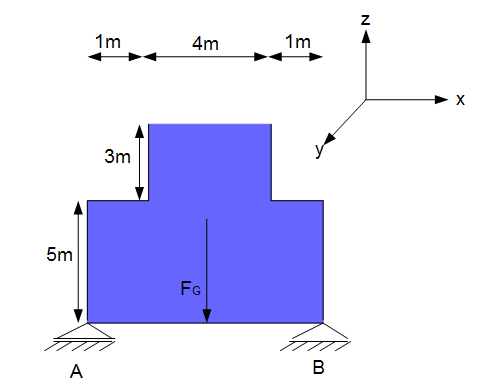
Wie groß ist die Gewichtskraft des Wassers? Wie groß ist die Druckkraft, die auf den Behälterboden wirkt? Wie groß sind die Lagerkräfte?
Gewichtskraft des Wassers
Die Gewichtskraft des Wassers wird bestimmt durch:
$F_G = \rho \; g \; V$.
Hier muss das gesamte Volumen des obigen Beckens berücksichtigt werden. Das Volumen ergibt sich u.a. durch:
$V = 5m \cdot 6m \cdot 1m + 3m \cdot 4m \cdot 1m = 42m^3$.
Die $b = y = 1m$ sind in der Aufgabenstellung nicht angegeben. Ist die Breite $y$ nicht angegeben, dann wird 1 m verwendet.
$F_G = \rho \; g \; V$.
Methode
$F_G = 999,97 \frac{kg}{m^3} \cdot 9,81 \frac{m}{s^2} \cdot 42m^3 = 412.007,64 N = 412 kN$.
Druckkraft auf Behälterboden
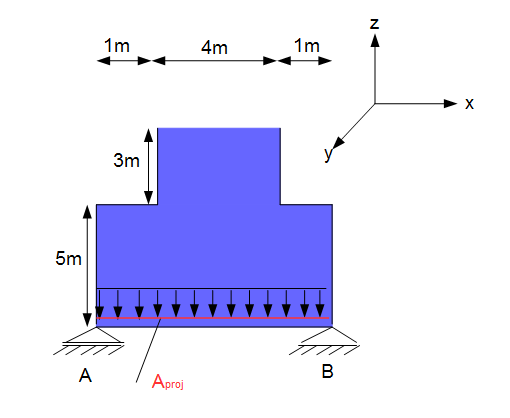
Um die Kraft zu bestimmen welche auf den Behälterboden wirkt, muss man zunächst den Druck bestimmen, welcher sich in dieser Tiefe ergibt:
$p(h) = \rho \; g \; h$
$p(h) = 999,97 \frac{kg}{m^3} \cdot 9,80 \frac{m}{s^2} \cdot 8 m = 78.477,65 Pa$.
Es muss dann der Druck für den gesamten Boden bestimmt werden. Hierzu muss die Fläche $x \cdot y$ betrachtet werden, da die Druckkraft in $z$-Richtung gesucht wird:
$A = x \cdot y = 6 m \cdot 1 m = 6m^2$.
Es gilt: $F = p \cdot A_{proj}$
Methode
$F_Z = 78.477,65 \frac{kg}{m \; s^2} \cdot 6m^2 = 470.865,90v \frac{kg \; m}{s^2} = 470,87 kN$.
Es wurde hier die Formel:
$F = p \cdot A_{proj}$ angwendet, welche aus dem Abschnitt Horizontalkraft bekannt ist. Hier war aber die Frage, welche Druckkraft am Behälterboden resultiert, weshalb hier die $z$-Richtung betrachtet wurde. Die projizierte Fläche $A_{proj}$ ist hier nicht wie bei der Horizontalkomponente eine Dreieckslast, sondern eine konstante Last, da der Boden des Beckens in jedem Punkt die gleiche Tiefe aufweist und demnach der Druck überall konstant ist. Es wirkt also nicht die Hälfte des Drucks auf den Boden, sondern der gesamte Druck, weshalb hier nicht der Schwerpunkt betrachtet wird. Da die Kraft in $z$-Richtung gesucht wird, ergibt sich die projizierte Fläche aus der $x$- und $y$-Richtung.
Merke
Betrachtet man bei der Formel $F = p \cdot A_{proj}$ die Kraft in $x$-Richtung (Horizontalkraft), so berechnet sich die projizierte Fläche aus der $y,z$-Richtung. Betrachtet man die Kraft in $z$-Richtung, so berechnet sich die projizierte Fläche aus der $x,y$-Richtung und bei Betrachtung der $y$-Richtung berechnet sich die projizierte Fläche aus der $x,z$-Richtung.
Bestimmung der Lagerkräfte
Zunächst einmal werden die Lagerkräfte aus der Gewichtskraft des Wassers bestimmt. Es sollen hier nur die vertikalen Kräfte bestimmt werden:
$\curvearrowleft A : B_v \cdot 6m - F_G \cdot 3 m$
Die Gewichtskraft greift mittig an, deswegen 3 m.
Methode
$B_v = F_G \frac{3m}{6m} = 412 kN \frac{3m}{6m} = 206 kN$.
$\curvearrowleft B: -A_v \cdot 6m + F_G \cdot 3m$
Methode
$A_v = F_G \frac{3m}{6m} = 412 kN \frac{3m}{6m} = 206 kN$.
Die Gewichtskraft des Wassers verteilt sich auf beide Lager.
Merke
Erinnerung: Ein Moment wird positiv, wenn sich das betrachtete Objekt gegen den Uhrzeigersinn um den Bezugspunkt dreht und negativ, wenn es sich im Uhrzeigersinn um den Bezugspunkt dreht.
Die zweite Möglichkeit besteht darin, die Kräfte aus der Druckkraft $F_Z$ auf den Boden zu bestimmen. Auch diese greift mittig an, da hier die rechteckige Last ihren Schwerpunkt in der Mitte aufweist und genau dort die Kraft $F_Z$ angreift (bei der Horizontalkraft war es so, dass diese bei 2/3 der Höhe angreift, da eine Dreieckslast vorlag und diese ihren Schwerpunkt bei 2/3 der Höhe hat):
$\curvearrowleft A : B_v \cdot 6m - F_Z \cdot 3 m$
$B_v = F_Z \frac{3m}{6m} = 470,87 kN \frac{3m}{6m} = 235,44 kN$.
$\curvearrowleft B: -A_v \cdot 6m + F_Z \cdot 3m$
$A_v = F_Z \frac{3m}{6m} = 470,87 kN \frac{3m}{6m} = 235,44 kN$.
Die Gewichtskraft des Wassers verteilt sich auf beide Lager.
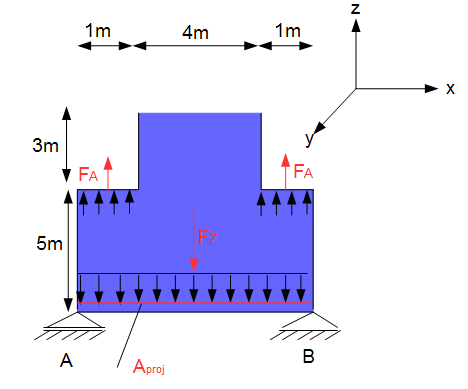
Es sind nun zwei unterschiedliche Werte für die Lager ermittelt worden. Wie kann das sein? Es muss bei der letzten Berechnungsweise noch zusätzlich die Auftriebskraft an den Seitenteilen berücksichtigt werden:
Es muss nun also die Auftriebskraft $F_A$ an den Seitenteilen berücksichtigt werden:
$F_A = p \cdot A_{proj}$.
Es wird zunächst die linke Seite betrachtet. Der Druck wird berechnet durch:
$p(h) = \rho \; g \; h = 999,97 \frac{kg}{m^3} \cdot 9,80 \frac{m}{s^2} \cdot 3 m = 29.429,12 Pa$.
Hier wurde die Höhe $h = 3m$ gewählt, da die Seitenteile 3 m tief liegen.
Die projizierte Fläche bestimmt sich durch:
$A_{proj} = x \cdot y = 1m \cdot 1m = 1m^2$.
Insgesamt ergibt sich für die Auftriebskraft der linken Seite:
$F_A^l = 29.429,12 \frac{kg}{m \; s^2} \cdot 1 m^2 = 29.429,12 N = 29,43 kN$.
Die rechte Seite besitzt dieselbe Auftriebskraft:
$F_{A}^r = 29,43 kN$.
Die erneute Berechnung der Lagerkräfte muss nun unter Berücksichtigung dieser Auftriebskräfte geschehen:
$\curvearrowleft A : B_v \cdot 6m - F_Z \cdot 3 m + F_A^l \cdot 0,5m + F_A^r \cdot 5,5m$
$B_v = F_Z \frac{3m}{6m} - F_A^l \cdot \frac{0,5m}{6m} - F_A^r \cdot \frac{5,5m}{6m} $
$B_v = 470,87 kN \frac{3m}{6m} - 29,43 kN \cdot \frac{0,5m}{6m} - 29,43 kN \cdot \frac{5,5m}{6m}= 206 kN$.
$\curvearrowleft B: -A_v \cdot 6m + F_Z \cdot 3m - F_A^l \cdot 5,5m - F_A^r \cdot 0,5m$
$A_v = F_Z \frac{3m}{6m} - F_A^l \cdot \frac{5,5m}{6m} - F_A^r \cdot \frac{0,5m}{6m} $
$A_v = 470,87 kN \frac{3m}{6m} - 29,43 kN \cdot \frac{5,5m}{6m} - 29,43 kN \cdot \frac{0,5m}{6m}= 206 kN$.
Die Lagerkräfte stimmen nun mit denen überein, welche aus der Gewichtskraft $F_G$ bestimmt worden sind.
Merke
Wichtig ist also, dass die Lagerkräfte aus der Gewichtskraft des Wassers berechnet werden können (einfache Methode). Oder eben aus den Druckkräften auf den Boden. Hier müssen aber noch zusätzlich die Auftriebskräfte an den Seitenteilen berücksichtigt werden (sofern vorhanden).
Weitere interessante Inhalte zum Thema
-
Vertikalkraft
Vielleicht ist für Sie auch das Thema Vertikalkraft (Hydrostatik) aus unserem Online-Kurs Strömungslehre interessant.
-
Druckkräfte auf eben geneigte nicht-rechteckige Flächen
Vielleicht ist für Sie auch das Thema Druckkräfte auf eben geneigte nicht-rechteckige Flächen (Hydrostatik) aus unserem Online-Kurs Strömungslehre interessant.