Inhaltsverzeichnis
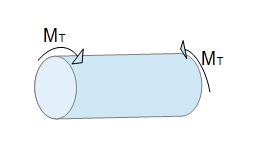
Der erste Untersuchungsgegenstand bei der Untersuchung von Torsion ist eine Welle mit einem konstanten Querschnitt über die gesamte Länge. Es handelt sich um eine Vollwelle, die an beiden Seiten durch das Torsionsmoment $ M_T $ belastet wird.
Führt man nun einen senkrechten Schnitt durch die Welle, so liegt an dieser Stelle ausschließlich das innere Torsionsmoment $M_T$ vor. Dieses führt zu Schubspannungen in der Schnittebene. Gegenstand dieser Untersuchung ist die Ermittlung der Spannungsverteilung im Inneren, die Verformung und die Verdrehung der Wellenenden gegeneinander.
Merke
Die Berechnung wird in drei Teile zerlegt:
Statik (Gleichgewichtsbedingungen), kinematische Gleichungen (Verformungen) und das Stoffgesetz (Hookesches Gesetz).
Vor dem Beginn der Berechnungen werden wieder Annahmen getroffen:
- Die Querschnitte bleiben unverformt.
- Die Querschnitte bleiben eben.
Aus den Annahmen kann man Folgendes ableiten:
1. Ein Punkt im Querschnitt verschiebt sich immer auf der Kreisbahn um die Drehachse, die durch den Kreismittelpunkt verläuft.
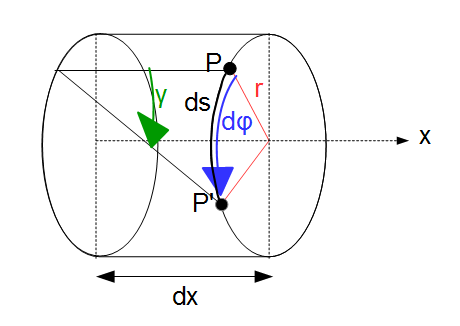
2. Nimmt man ein sehr dünnes Scheibchen [Dicke dx] aus der Welle heraus, so sieht man, dass sich die beiden Kreisflächen um einen Winkel $ d \varphi $ relativ gegeneinander verdrehen.
3. Ein Punkt legt auf der rechten Kreisfläche der entnommenen Scheibe einen Weg $ ds = r d\varphi $ zurück, analog dazu auf der linken Kreisfläche. $r $ steht hierbei für den Kreisradius.
4. Alternativ lässt sich der Weg eines Punktes auch mit Hilfe des Winkels $\gamma$ bestimmen. Siehe hierzu die obige Abbildung.
Es gilt: $ r d\varphi = \gamma dx $
Stellt man diese Gleichung um, erhält man:
$\frac{d\varphi}{dx} = \frac{\gamma_a}{r}$
Auf der linken Seite der Gleichung steht nun der Ausdruck für die Ableitung des Verdrehwinkels $\varphi $ nach $x$. Diesen Ausdruck bezeichnet man auch als Verdrillung $\varphi' $ bzw. $\vartheta$:
$\varphi' = \vartheta = \frac{d\varphi}{dx} $
Der Zusammenhang zwischen Gleitwinkel $\gamma $ und Schubspannung $\tau $ lässt sich unter Verwendung des Hookeschen Gesetzes ermitteln:
$\tau = G \gamma = G \; \vartheta \; r $
Merke
Diese Gleichung zeigt, dass eine Zunahme des Radius $ r $ auch zu einer linearen Zunahme der Schubspannungen führt. Daher sind die Schubspannungslinien konzentrische Kreise.
Bestimmung der Verdrillung
Um nun eine genau Aussage bezüglich der Schubspannung treffen zu können, ist es vorab notwendig die Verdrillung $\vartheta $ zu bestimmen.
Davon ausgehend, dass die Schubspannungen Momente hervorrufen, integriert man diese über die gesamte Kreisfläche. Als Resultat erhält man dann das resultierende Schnittmoment, welches dem äußeren Moment $ M_T $ entspricht:
$ M_T = \int_A \tau\; r \; dA = \int_A G \vartheta \; r^2 \; dA = G \vartheta \int_A r^2 dA $
Hierbei stellt der Ausdruck $\int_A r^2 = I_P $ das polare Flächenträgheitsmoment dar, womit sich die obige Gleichung umschreiben lässt zu:
$ M_T = G\; I_p \; \vartheta $.
Löst man diese Gleichung nun noch nach $\varphi' $ auf, so liefert dies die Verdrillung mit
Methode
$\vartheta = \frac{M_T}{G I_P} $ Verdrillung
mit
$\vartheta = \frac{d\varphi}{dx}$
$M_T$ Torsionsmoment
$G$ Schubmodul
$I_P$ polares Flächenträgheitsmoment
Es stellt sich nun heraus, dass die Verdrillung von drei Parametern abhängt:
1. Torsionsmoment $ M_T $,
2. Materialparameter $ G $,
3. Polares Flächenträgheitsmoment $ I_P$.
Bestimmung der Schubspannung
Für die vom Radius abhängige Spannung erhält man durch Einsetzen von
$\vartheta = \frac{M_T}{G I_P}$
in
$\tau = G \gamma = G \; \vartheta \; r $
den Ausdruck
Methode
$\tau(r) = \frac{M_T}{I_P} \cdot r $ Schubspannungen
Berechnung der Verdrehung
Wenn in einem zylindrischen Stab an jeder Stelle ein identisches Torsionsmoment wirkt, so ist die spezifische Verdrehung $\frac{d\varphi}{dx} = \vartheta$ durchweg konstant.
$\vartheta = \text{konstant}$
$\vartheta = \frac{d\varphi}{dx}$
Trennung der Veränderlichen:
$\vartheta \; dx = d\varphi$
Intergation, wobei $\vartheta = const$:
$\vartheta \int_0^x d_x = \int_{\varphi_0}^{\varphi(x)} d\varphi$
$\vartheta \cdot x = \varphi(x) - \varphi_0$
Methode
$\rightarrow \varphi(x) = \varphi_0 + \vartheta \cdot x $
Wählt man nun eine Stelle $x$ mit dem Abstand $ l$ [hier: Wellenende] aus, so gilt:
$\varphi(l) = \varphi_0 + \vartheta \cdot l $
Die Anfangsverdrehwinkel $\varphi_0 $ sind dann entsprechend
$\varphi_0 = \varphi(x=0) $.
Merke
Die Differenz aus beiden Wellenenden wird beschrieben durch:
$\triangle \varphi = \varphi(l) - \varphi_0$
$\triangle \varphi = \vartheta \cdot l $
Setzt man nun noch den Ausdruck für die Verdrillung $ \vartheta $ ein, liefert dies:
Methode
$\triangle \varphi = \frac{M_T \cdot l}{G \cdot I_P} $ Endverdrehung bei konstanter Verdrillung
Ist die spezifische Verdrehung (bzw. Verdrillung) $\triangle \varphi$ nicht konstant, so kann die Lösung mit Hilfe von Integration erfolgen. Es gilt
$\vartheta = \frac{d\varphi}{dx}$
Einsetzen in (wobei $\vartheta$ nicht mehr konstant ist):
$\vartheta = \frac{M_T}{G I_P} $
Ergibt:
$\frac{d\varphi}{dx} = \frac{M_T}{G I_P}$
Trennung der Veränderlichen:
$d\varphi = \frac{M_T}{G I_P} \; dx$
Integration:
$\int_{\varphi_0}^{\varphi(x)} d\varphi = \int \frac{M_T}{G I_P} \; dx$
Methode
$\varphi(x) = \varphi_0 \int_0^x \frac{M_T(x)}{G(x)I_P(x)} dx $ Endverdrehung bei nicht-konstanter Verdrillung
Bestimmung des polaren Flächenträgheitsmoments
Das polare Flächenträgheitsmoment ist nur dann veränderlich, wenn auch der Durchmesser der Welle variiert.
Für das polare Flächenträgheitsmoment gilt:
Methode
$ I_P = \int_A r^2 dA = \int_{r=0}^r r^2 2\pi r \; dr = \frac{\pi r^4}{2} $ polares Flächenträgheitsmoment
Bestimmung der Maximalspannung
Die maximale Spannung liegt am Rand der Welle. Davon ausgehend, dass der Radius die Länge $r =R$ besitzt, folgt:
Methode
$\tau_{max} = \tau_{r} = \frac{M_T}{I_P}\cdot R $ Maximale Schubspannung
Widerstandsmoment
Eine andere Möglichkeit zur Bestimmung der maximalen Spannung ist die Hinzunahme des Widerstandsmoments $W_T$:
Methode
$ \tau_{max} = \frac{M_T}{W_T} $ Maximale Schubspannung (Widerstandsmoment)
mit
$W_T = \frac{I_P}{R} = \frac{\pi r^3}{2}$
$\\$
Merke
$ I_T = $ Torsionsflächenträgheitsmoment,
$ GI_T = $ Torsionssteifigkeit.
Beim Kreisquerschnitt entspricht $ I_T = I_P $.
Weitere interessante Inhalte zum Thema
-
Differentialgleichungen mit getrennten Variablen
Vielleicht ist für Sie auch das Thema Differentialgleichungen mit getrennten Variablen (Gewöhnliche Differentialgleichungen) aus unserem Online-Kurs Analysis und Gewöhnliche Differentialgleichungen interessant.
-
Einführung in die technische Mechanik
Vielleicht ist für Sie auch das Thema Einführung in die technische Mechanik (Grundlagen der Technischen Mechanik) aus unserem Online-Kurs Technische Mechanik 1: Statik interessant.