Änderung der Zielfunktionskoeffizienten

In diesem Abschnitt wird mittels Sensitivitätsanalyse gezeigt, in welchem Bereich die Zielfunktionswerte variiert werden können, ohne dass die Optimallösung des Optimierungsproblems ihre Optimalitätseigenschaft verliert, d.h. ohne dass ein zusätzlicher Basisaustausch bzw. Simplexschritt notwendig wird. Das bedeutet also, dass das Optimaltableau in der Form bestehen bleibt (Basisvariablen, Werte), wenn die Koeffizienten Zielfunktion in einem bestimmten Bereich variiert werden. Dabei gilt der Schwankungsbereich der Zielfunktionswerte nur für das Ausgangstableau. Werden also im Ausgangstableau die Zielfunktionswerte in einem bestimmten Bereich variiert (immer ein Zielfunktionswert, wobei die anderen konstant gehalten werden), so ergibt sich das gleiche Optimaltableau, wie ohne Variation der Werte. 

Vorgehensweise: Schwankungsbereich Zielfunktionskoeffizienten

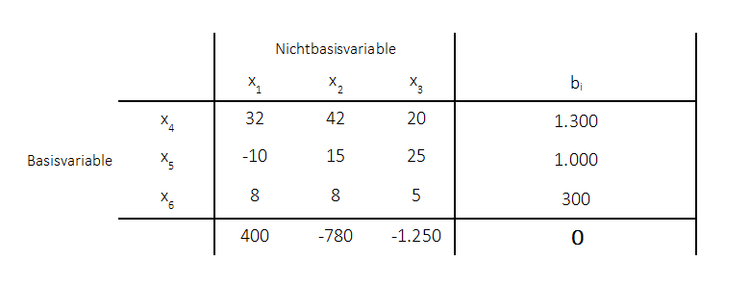
1. Es wird zunächst das Ausgangstableau betrachtet:

Ausgangstableau

Die Zielfunktionskoeffizienten im Ausgangstableau $c_j$ werden wie folgt definiert:

$c_1 = -400$   

$c_2 = 780$     

$c_3 = 1.250$.

Die zu den Zielfunktionskoeffizienten zugehörigen Variablen $x_j$ sind:

$x_1$ für $c_1$,

$x_2$ für $c_2$,

$x_3$ für $c_3$.

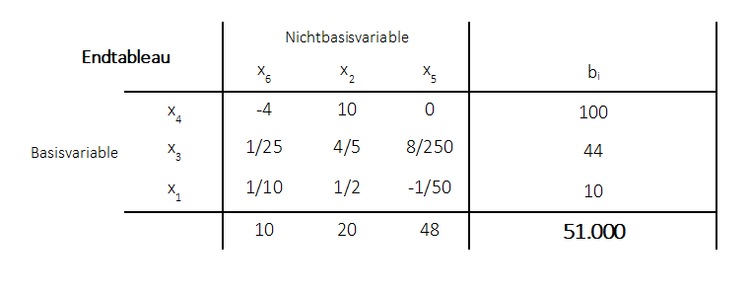
2. Danach wird das Optimaltableau herangezogen:

Optimaltableau

Es wird nun geschaut, wo sich die im Ausgangstableau befindlichen Nichtbasisvariablen im Optimaltableau befinden. Im Ausgangstableau sind die Nichtbasisvariablen $x_1$, $x_2$ und $x_3$. Im Optimaltableau stellen $x_1$ und $x_3$ Basisvariablen dar, $x_2$ hingegen ist Nichtbasisvariable. Es muss nun bei der Berechnung der unterschieden werden zwischen Basisvariablen und Nichtbasisvariablen:

Basisvariablen

Ist die im Ausgangstableau befindliche Nichtbasisvariable im Optimaltableau eine Basisvariable, so muss folgende Berechnung durchgeführt werden:

Nichtbasisvariablen

Ist die im Ausgangstableau befindliche Nichtbasisvariable im Optimaltableau ebenfalls eine Nichtbasisvariable, so muss folgende Berechnung durchgeführt werden:

Schwankungsbereich der Zielfunktionskoeffizienten

Den Schwankungsbereich ermittelt man dann mittels folgendem Intervall:

Vorgehensweise

Die genaue Vorgehensweise wird im Weiteren ausführlich behandelt. Dazu sei das obige Ausgangs- und Optimaltableau gegeben.

1. Zunächst sind die Nichtbasisvariablen aus dem Ausgangstableau und die dazugehörigen Zielfunktionskoeffizienten zu bestimmen:

$c_1 = -400$   für $x_1$

$c_2 = 780$    für $x_2$

$c_3 = 1.250$   für $x_3$.

2. Danach wird geschaut wo sich die Variablen im Optimaltableau befinden. $x_1$ und $x_3$ sind Basisvariablen, $x_2$ ist eine Nichtbasisvariable. Es werden zunächst die Basisvariablen betrachtet.

• $x_1$ = Basisvariable:

Die Berechnung wird anhand der beiden obigen Formeln durchgeführt

Es wird zunächst der Wert $c_1^-$ berechnet. Hierfür werden alle Koeffizienten im Optimaltableau betrachtet, die sich in der Zeile von $x_1$ befinden und größer als Null sind. Die dazugehörigen Zielfunktionswerte stehen dann unter diesen Koeffizienten. Größer als Null sind die Koeffizienten: $a_{31}^* = \frac{1}{10}$ mit $c_1^* = 10$ und $a_{32}^* = \frac{1}{2}$ mit $c_2^* = 20$. Existieren keine Werte größer als Null, so nimm $c_1^-$ den Wert $\infty$ an. Einsetzen in die Formel ergibt:

$c_1^- := min \{ \frac{10}{\frac{1}{10}} ; \frac{20}{\frac{1}{2}} \} = 40$

Danach wird $c_1^+$ berechnet.

Hierfür werden alle Koeffizienten im Optimaltableau betrachtet, die sich in der Zeile von $x_1$ bfinden und kleiner als Null sind. Existieren keine Werte kleiner als Null, so nimmt $c_1^+$ den Wert $\infty$ an. Es existieren aber Werte kleiner als Null, und zwar $a_{33}^* = -\frac{1}{50}$ mit $c_3^* = 48$:

$c_1^+ := min \{ -\frac{48}{-\frac{1}{50}} \} = 2.400$

Der Schwankungsbereich wird ermittelt mit dem Intervall:

$[c_j - c_k^- \; , \; c_j + c_k^+]$      

mit  $c_j = c_1 = -400$ (Zielfunktionswert im Ausgangstableau für $x_1$)

Es ergibt sich ein Schwankungsbereich für $c_1 $ von:

$[-400 - 40; -400 + 2.400]$

Der Zielfunktionswert $c_1$ darf im Ausgangstableau die Werte von -440 bis 2.000 annehmen, ohne dass die Basislösung die Optimalitätseigenschaft verliert, d.h. also ohne dass ein Basistausch erforderlich wird.

• $x_3$ = Basisvariable:

$c_3^- := min \{ \frac{10}{\frac{1}{25}} ; \frac{20}{\frac{4}{5}} ; \frac{48}{\frac{8}{250}} \} = 25$

$c_3^+ := \infty$   (Es existieren keine negativen Koeffizienten im Optimaltableau)

Der Schwankungsbereich liegt demach für $c_3$ bei:

$[1.250 - 25; 1.250 + \infty]$

Der Zielfunktionswert $c_3$ darf im Ausgangstableau die Werte ab 1.225 annehmen, ohne dass die Basislösung die Optimalitätseigenschaft verliert, d.h. also ohne dass ein Basistausch erforderlich wird.

• $x_2$ = Nichtbasisvariable:

$x_2$ stellt im Optimaltableau eine Nichtbasisvariable dar. Die Berechnung erfolgt zu:

$c_2^- = \infty$

$c_2^+ = c_2^* = 20$  $c_2^+$ nimmt den Wert an, den $c_2^*$ im Optimaltableau als Zielfunktionswert besitzt.

Der Schwankungsbereich ergibt sich zu:

$[780 - \infty; 780 + 20]$

Der Zielfunktionswert $c_2$ darf im Ausgangstableau die Werte bis 800 annehmen, ohne dass die Basislösung die Optimalitätseigenschaft verliert, d.h. also ohne dass ein Basistausch erforderlich wird.

• $x_4$: Schlupfvariable

Ist in dem Optimaltableau eine Schlupfvariable in der Basis gegeben, so kann man auf für diese die obigen Berechnungen anführen und einen Schwankungsbereich ermitteln:

$c_1^- := min \{ \frac{20}{10} \} = 2$

$c_1^+ := min \{ -\frac{10}{-4} \} = 2,5$

Der Schwankungsbereich ergibt sich zu (bei Schlupfvariablen ist der Zielfunktionswert $c_j$ immer Null):

$[0 - 2; 0 + 2,5]$

Eine Schlupfvariable besitzt immer den Zielfunktionswert Null. Befindet sich eine Schlupfvariable im Optimaltableau aber in der Basis, so besitzt diese auch einen Schwankungsbereich. Die Schulpfvariable $x_4$ kann demnach in die Zielfunktion mit den Werten zwischen -2 und 2,5 eingehen, ohne dass die Basislösung die Optimalitätseigenschaft verliert, d.h. also ohne dass ein Basistausch erforderlich wird.