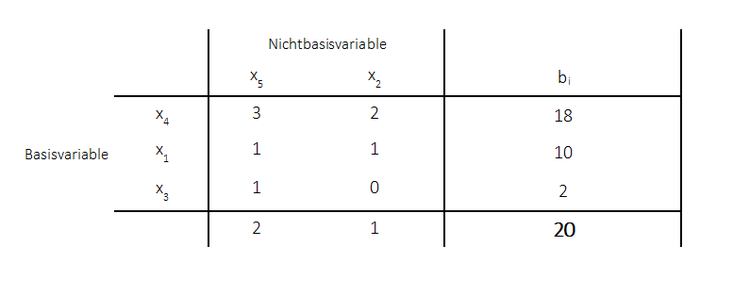
Nachdem nun alle künstlichen Variablen aus der Basis entfernt wurden, wird als nächstes das primale Simplexverfahren angewendet, damit aus der zulässigen Lösung eine optimale Lösung gewonnen wird. Es müssen noch zwei weitere Simplexschritte durchgeführt werden, damit am Ende das folgende Tableau resultiert:
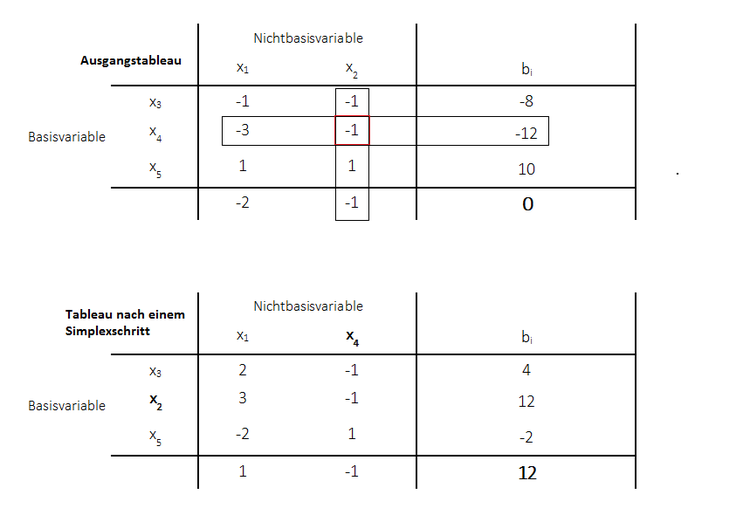
Die künstlichen Variablen sind bereits zu Beginn aus dem Tableau entfernt worden. Danach ist nach dem primalen Simplexalgorithmus zunächst die Pivotspalte (kleinster negativer Wert der Zielfunktionszeile, da beide Werte gleich groß waren, konnte man sich einen beliebigen wählen) bestimmt worden. Danach die Pivotzeile indem der kleinste Quotient aus rechter Seite und positiven Werten der Pivotspalte ausgewählt worden ist. Nach Durchführung eines Simplexschrittes war noch ein negativer Wert (unter $x_4$) vorhanden. Das primale Simplexverfahren musste also nochmals durchgeführt werden. Am Ende resultiert nun das obige Tableau mit positiven Werten in der Zielfunktionszeile. Demnach ist hier die Optimallösung erreicht. Diese beträgt:
$x_4 = 18$, $x_1 = 10$, $x_3 = 20$ und $x_2 = y_1 = y_2 = x_5 = 0$ mit dem Zielfunktionswert $z = 20$.
$z = (2 + 4M) \cdot 10 + (1 + 2M) \cdot 0 - M \cdot 18 - M \cdot 2 - 20M$
$z = 20 + 40 M - 18M - 2M - 20M = 20$.
Weitere interessante Inhalte zum Thema
-
Duales Simplexverfahren: Simplexschritte
Vielleicht ist für Sie auch das Thema Duales Simplexverfahren: Simplexschritte (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.