Inhaltsverzeichnis
Definition der Stepping-Stone-Methode
Die Stepping-Stone-Methode ist ein Optimierungsverfahren für Transportprobleme und dient der Bestimmung einer optimalen Lösung bei welcher die Transportkosten minimal sind. Ausgehend von der Ausgangslösung nach dem Matrixminiumverfahren, erfolgt in diesem Abschnitt die iterative Verbesserung der Ausgangslösung hin zu einer optimalen Lösung durch die Stepping-Stone-Methode.
Methode
Stepping-Stone-Methode
1. Es wird ein nicht belegtes Feld ausgewählt. In dieses Feld setzt man die fiktive Menge $x_{ij} = +1$. Ausgehend von diesem Feld schreitet man waagerecht (nach rechts oder links) voran zu einem belegten Feld, welches aber ein unter oder über sich (senkrecht) belegtes Feld aufweist. Die Menge des belegten Feldes wird fiktiv um $x_{ij} = 1$ reduziert.
2. Man schreitet dann von diesem Feld zu dem senkrecht belegten Feld, welches aber wiederum ein rechts oder links liegendes (waagrechtes) belegtes Feld oder das Ausgangsfeld aufweisen muss. Die Menge des belegten Feldes wird fiktiv um $x_{ij} = 1$ erhöht.
Die Schritte 1-2 werden solange wiederholt, bis man wieder am Ausgangsfeld $x_{ij}$ angekommen ist.
3. Danach werden die Kosten $c_{ij}$ der abgegangenen Felder miteinander verrechnet und damit der Zykluswert $\triangle z$ bestimmt. Die Kosten der Felder mit +1 werden addiert, die Kosten der Felder mit -1 subtrahiert. Am Ende wird der Zykluswert $\triangle z$ auf das Statfeld in die rechte unteren Ecke notiert.
4. Ist $\triangle z < 0$, so kann eine Verbesserung der Ausganglösung erfolgen. Es wird dann eine Mengenverschiebung vorgenommen. Es wird dafür die minimale Menge auf dem Pfad mit den Felder die um 1 reduziert wurden gewählt und diese Menge an das Startfeld verschoben. Alle anderen Mengen auf dem Pfad müssen dann so angepasst werden, dass die Mengen der Felder mit +1 mit dieser Menge addiert werden und die Mengen der Felder mit -1 mit dieser Menge subtrahiert. Es werden dann wieder für alle unbelegten Felder (auch die bereits eine Zykluszahl erhalten) neue Zyklen bestimmt.
Ist $\triangle z > 0$ so kann keine Verbesserung der Ausgangslösung erfolgen. Es wird dann das nächste nicht belegte Feld betrachtet und die Schritte 1-4 wiederholt.
Die Schritte werden solange wiederholt bis alle $\triangle z > 0$.
Vorgehensweise bei der Stepping-Stone-Methode
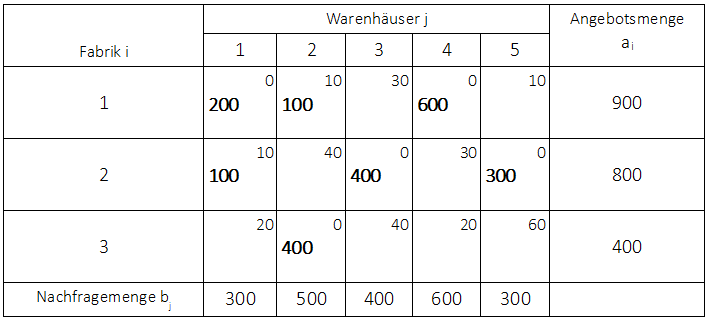
Die Vorgehensweise soll anhand der Ausgangslösung nach dem Matrixminimumverfahren durchgeführt werden:
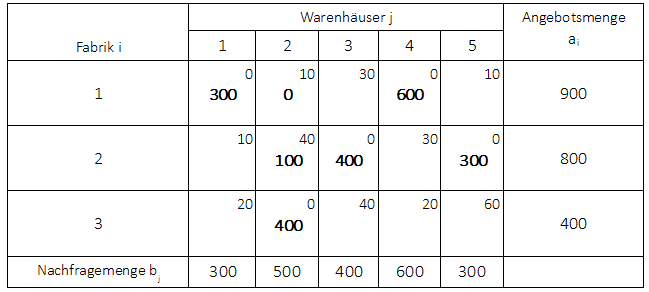
Auswahl eines nicht belegten Feldes. (Hinweis: Das Feld $x_{12}$ besitzt zwar Null Mengen, ist aber trotzdem belegt, da $m + n -1 = 3 + 5 - 1 = 7$ Basisvariablen gegeben sein müssen). Es wird beliebig das unbelegte Feld $x_{13}$ gewählt.
Die Vorgehensweise ist nun wie folgt. Es muss zunächst waagerecht vorgegangen werden zu einem belegten Feld. Danach wird abwechseld senkrecht und waagerecht von belegtem Feld zu belegtem Feld vorgegangen, bis wieder das Startfeld $x_{13}$ erreicht wird.
Es wird zunächst vom Feld $x_{13}$ waagerecht vorgegangen. Dabei wird ein belegtes Feld angesteuert. Dieses belegte Feld muss aber ein belegtes Feld senkrecht von sich aufweisen und das senkrechte Feld wieder ein belegtes Feld waagerecht etc. So dass ein Zyklus entsteht. Das Feld $x_{12}$ besitzt zwei senkrecht unter sich liegende Felder $x_{22}$ oder $x_{32}$. Da man aber nur vom Feld $x_{22}$ wieder waagerecht weiter zu einem belegten Feld schreiten kann, wird dieses Feld für den Zyklus gewählt. Von diesem Feld kann man dann entweder das belegte Feld $x_{23}$ oder $x_{25}$ ansteuern. Das Feld $x_{25}$ besitzt aber kein senkrechtes belegtes Feld über oder unter sich. Deswegen wird das Feld $x_{23}$ angeseteuert und dann wieder zum Startfeld zurück.
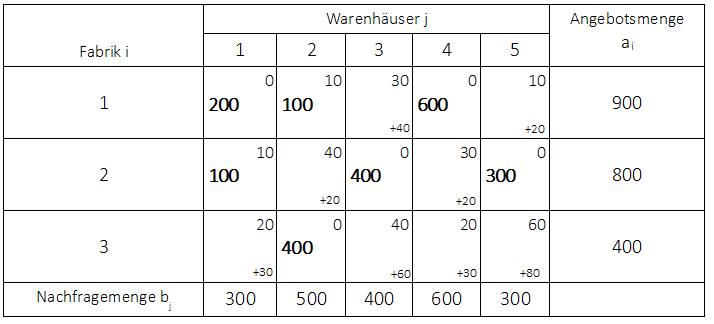
In der obigen Grafik ist der Zyklus aufgeführt. Beginnend bei dem unbelegten Feld $x_{13}$ werden danach nur noch belegte Felder angesteuert. Dabei muss immer ein Richtungswechsel von waagrecht zu senkrecht und umgekehrt stattfinden. Der Zyklus wird wieder beim Startfeld beendet. Das Startfeld erhält die fiktive Menge +1. Danach werden immer abwechselnd die belegten Felder mit -1 und +1 belegt. Es wird dann $\triangle z$ bestimmt, indem die Kosten für die Felder mit +1 addiert werden und die Kosten mit Felder -1 subtrahiert:
$\triangle z = +30 - 10 + 40 - 0 = 60$.
Da $\triangle z > 0$ kann hier keine Verbesserung der Ausgangslösung vorgenommen werden. Der Zykluswert wird an die untere rechte Ecke des Startfeldes geschrieben und das nächste nicht belegte Feld betrachtet.
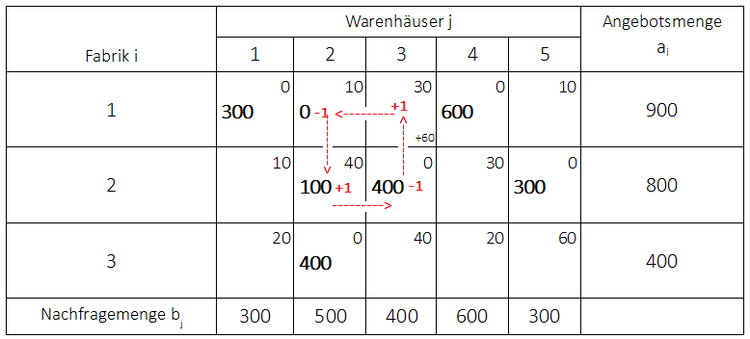
Es wurde als Startfeld das unbelegte Feld $x_{15}$ gewählt. Der Zykluswert beträgt:
$\triangle z = 10 - 10 + 40 - 0 = 40$.
Auch hier ist keine Verbesserung der Ausgangslösung zu erreichen.
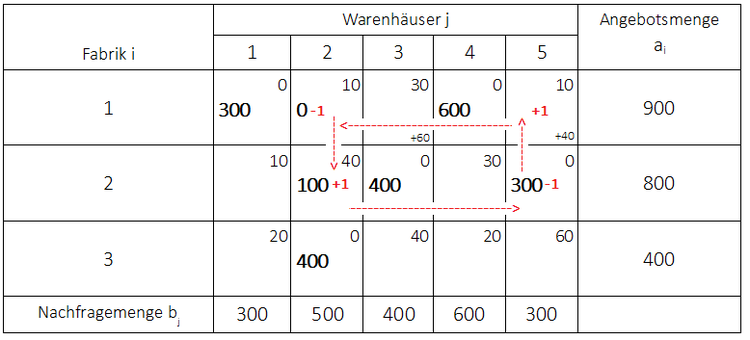
Es wurde als Startfeld das unbelegte Feld $x_{21}$ gewählt. Der Zykluswert beträgt:
$\triangle z = 10 - 10 + 40 - 0 = -20$.
Da $\triangle z < 0$, kann hier eine Verbesserung der Ausgangslösung stattfinden. Es wird nun die minimale Menge mit -1 auf dem Zyklus gewählt. Diese beträgt $x_{22} = 100$. Diese wird nun auf das Startfeld gesetzt. Alle anderen Mengen müssen nun so angepasst werden, dass die Angebots-und Nachfragemengen eingehalten werden. Das bedeutet also, dass überall dort wo eine -1 steht die 100 Mengen abgezogen werden und überall dort wo eine +1 steht die 100 Mengen addiert werden:
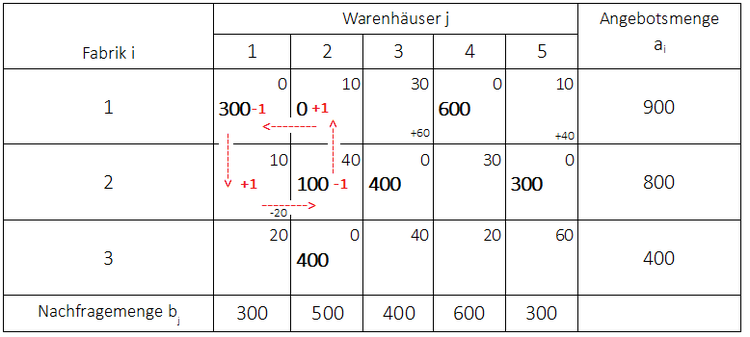
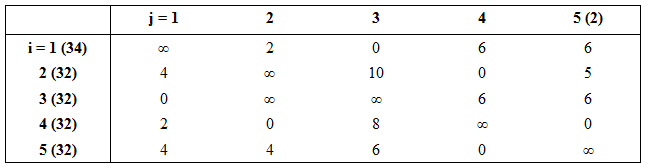
Nachdem nun die Mengenverschiebung von $x_{22}$ (jetzt ein unbelegtes Feld) zu $x_{21}$ (jetzt ein belegtes Feld) stattgefunden hat, müssen wieder alle unbelegten Felder betrachtet werden, d.h. die bereits berechneten Zykluswerte muss erneut berechnet werden, da sich neue Zyklen ergeben. In der folgenden Grafik sind die Zykluswerte der einzelnen Felder aufgeführt:
Alle weiteren Zykluswerte sind größer als Null, das bedeutet also, dass hier die optimale Lösung gefunden ist. Es ist zulässig, dass sich bei der Ermittlung der Zyklen die Pfeile für einen Zyklus überschneiden. Bei den Zykluswerte für die Felder $x_{33}$ und $x_{35}$ ergeben sich solche Überschneidungen der Pfeile.
Die gesamten Transportkosten können nun bestimmt werden, indem die Ausgangskostenmatrix herangezogen wird:
Lösung der Stepping-Stone-Methode
Die gesamten minimalen Transportkosten ergeben sich zu:
$K = 200 \cdot 140 + 100 \cdot 150 + 100 \cdot 130 + 400 \cdot 120 + 400 \cdot 140 + 600 \cdot 150 + 300 \cdot 130 = 289.000$.
Weitere interessante Inhalte zum Thema
-
Drehimpuls
Vielleicht ist für Sie auch das Thema Drehimpuls (Impuls und Stoß) aus unserem Online-Kurs Physik interessant.
-
Begrenzte Enumeration
Vielleicht ist für Sie auch das Thema Begrenzte Enumeration (Kombinatorische Optimierung) aus unserem Online-Kurs Operations Research 2 interessant.