Höhere Mathematik 1: Analysis und Lineare Algebra online lernen


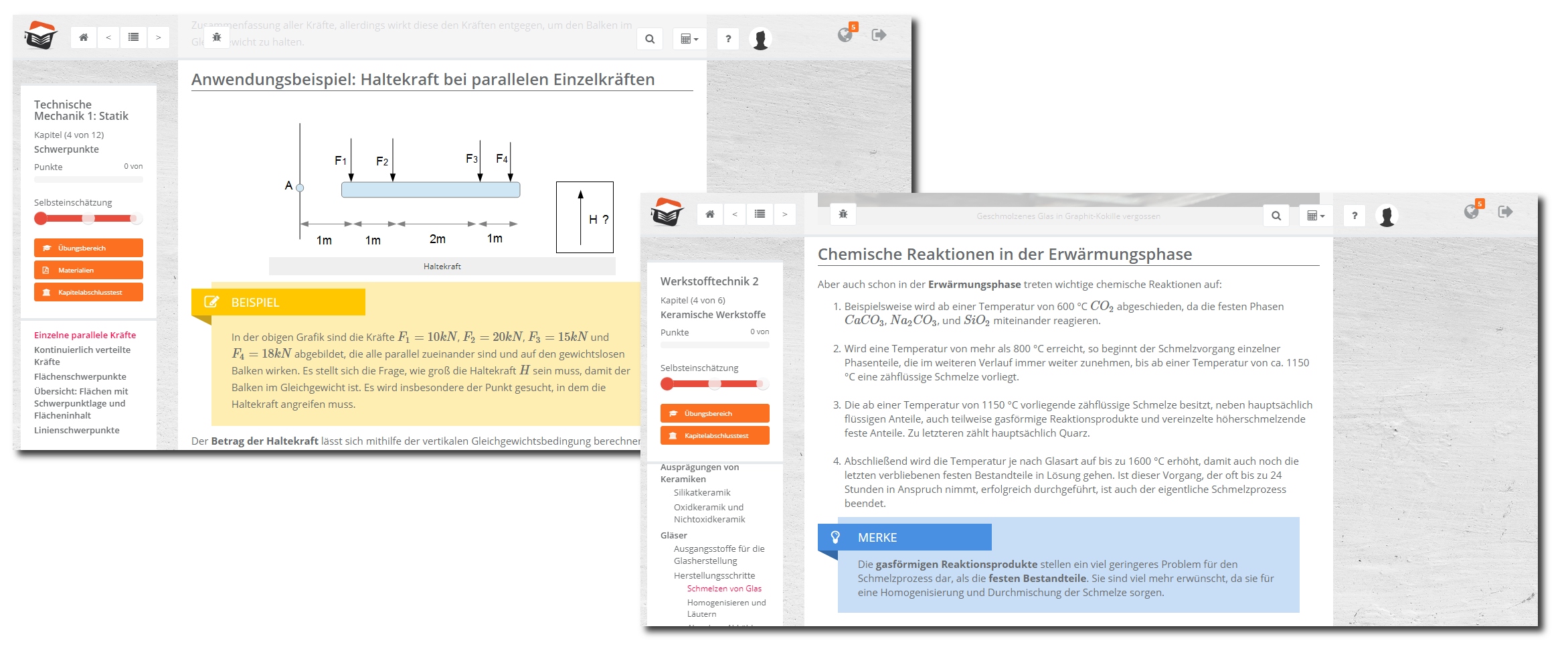
Die Höhere Mathematik 1 (oder Höhere Mathematik A) stellt eines der wichtigsten Studienfächer im Grundstudium eines Wirtschaftsingenieurs dar. Es vermittelt grundlegendes mathematisches Wissen, welches Ihnen im weiteren Verlauf Ihres Studiums immer wieder in anderen Studienfächern begegnen wird. Daher haben wir diesen Kurs entwickelt um Ihnen einen sicheren Weg dahin zu ebnen.

Im Eingangskapitel werden Sie ausführlich mit der Mengenlehre und den Reellen Zahlen vertraut gemacht. Dieses umfasst u.a. den Umgang mit Mengen sowie die Rechenkenntnisse zu Beträgen, Intervallen und Schranken.

Anschließend befassen wir uns mit der Vektorrechnung. Hier stehen besonders die Vektoraddition, Vektorsubtraktion und die Multiplikation von Vektoren im Mittelpunkt. Anhand von ausführlichen Beispielen erklären wir Ihnen den Unterschied von Skalarprodukten, Vektorprodukten sowie Spatprodukten. Im Kapitel Komplexe Zahlen werden die Grundrechenarten komplexer Zahlen sowie Nullstellen von Polynomen behandelt. Den Unterschied zwischen rationalen und nicht rationalen Funktionen im Kapitel Elementare Funktionen erklären wir Ihnen schrittweise und liefern Ihnen, wie zu beinahe jedem Kurstext, Übungsaufgaben mit Hilfe derer Sie ihren Wissensstand überprüfen können.

In der sich anschließenden Differentialrechnung thematisieren wir detailliert Ableitungen, Wendepunkte, Extremwerte, Mittelwertsätze, Monotonie sowie Konvexität von Funktionen. Ein Abschnitt widmet sich ausführlich der Regel von de l'Hospital und dem Näherungsverfahren zur Nullstellenberechnung nach Newton.

Wie Sie bestimmte, unbestimmte sowie uneigentliche Integralen voneiandner unterscheiden sowie berechnen können, veranschaulichen wir Ihnen im Kapitel Integralrechnung. Ferner behandeln wir die partielle Integration von Funktionen.

Mit der Linearen Algebra befassen wir uns schließlich im letzten Kapitel. Hierbei geht es vor allem um die Matrizenmultiplikation, die invertierbarber Matrix, das Gauß Eliminationsverfahren, den Rang einer Matrix, die Bestimmung der Determinanten nach Laplace und Cramer sowie die Berechnung der Eigenwerte und Eigenvektoren.

Nach Abschluss dieses Kurses können Sie beruhigt in die Klausur gehen und erfahren einen vereinfachten Einstieg in andere technisch-mathematische Studienfächer.
einmalig 39,00 €
Zur Kasse
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Online-Kurs Top AngebotTrusted Shop

Vorteile im Überblick

  • Über 120 Dokumente und mehr als 210 Übungen vermitteln Ihnen umfassend alles Wissenswerte.

    Im Kurs sind darüber hinaus 22 Videos enthalten, in denen die wichtigsten Themen anschaulich zusammengefasst werden. Insgesamt knapp 2,5 Stunden Videomaterial steigern Ihren Lernerfolg und sorgen nebenbei für Abwechslung.

  • Schon mehrere tausend Kursteilnehmer haben sich für unsere Online-Kurse entschieden. Wir haben über viele Jahre Erfahrungen gesammelt und unsere Kursoberfläche stetig verbessert.
  • Das Internet bietet Ihnen weitreichende Möglichkeiten: Lernen, wann und wo Sie möchten. Und daneben gibt es bei uns zahlreiche Features, die zum schnelleren und besseren Lernerfolg beitragen.
einmalig 39,00 €
Zur Kasse
Online-Kurs Top AngebotTrusted Shop
Diese Themen werden im Kurs behandelt:

[Bitte auf Kapitelüberschriften klicken, um Unterthemen anzuzeigen]

  • Grundlagen: Mengenlehre und reelle Zahlen
    • Einleitung zu Grundlagen: Mengenlehre und reelle Zahlen
    • Kurseinführung
    • Mengenlehre
      • Einführung in die Mengenlehre
      • Teilmengen
      • Mengenoperationen
        • Vereinigung von Mengen
        • Durchschnitt von Mengen
        • Differenz von Mengen
        • Komplementärmengen
        • Produktmengen
        • Übungsbeispiele zur Mengenlehre
      • Rechenregel für Mengen
        • Kommutativgesetz
        • Assoziativgesetz
        • Distributivgesetz
        • Regel von de Morgan
    • Reelle Zahlen
      • Einleitung zu Reelle Zahlen
      • Bezeichnung reeller Zahlen
      • Ungleichungen
        • Einleitung zu Ungleichungen
        • Beispiele: Betragsungleichungen, Bruchungleichungen
      • Intervalle
      • Schranken (Supremum, Infimum)
      • Beträge
      • Vollständige Induktion
        • Einleitung zu Vollständige Induktion
        • Beispiele: Vollständige Induktion
      • Fakultät und Binomialkoeffizienten
    • Anwendungsbeispiele: Mengenlehre und reelle Zahlen
  • Vektorrechnung
    • Einführung in die Vektorrechnung
      • Einleitung zu Einführung in die Vektorrechnung
      • Addition von Vektoren
      • Subtraktion von Vektoren
      • Skalieren von Vektoren
      • Einheitsvektor, Länge von Vektoren
      • Dreiecksungleichung
    • Das Skalarprodukt
      • Skalarprodukt und Winkel
      • Zerlegung von Vektoren
      • Rechengesetze für das Skalarprodukt
    • Das Vektorprodukt
    • Das Spatprodukt
    • Übungsaufgaben zur Vektorrechnung
    • Geraden im Raum
      • Einleitung zu Geraden im Raum
      • Identische Geraden
      • Parallele Geraden
      • Schnittpunkt zweier Geraden
      • Windschiefe Geraden
      • Abstände von Geraden/Punkten
      • Übungsaufgaben zu Geraden im Raum
  • Matrizen
    • Einleitung zu Matrizen
    • Addition und Subtraktion von Matrizen
    • Multiplikation mit Zahlenwerten bei Matrizen
    • Rechenregeln für Matrizen
    • Matrizenmultiplikation
    • Gauß Eliminationsverfahren
    • Invertierbare Matrix
    • Rang einer Matrix
    • Determinanten
      • Einleitung zu Determinanten
      • Laplacescher Entwicklungssatz
      • Cramersche Regel
    • Eigenwerte und Eigenvektoren
      • Eigenwerte
      • Eigenvektoren
      • Diagonalmatrix
      • Diagonalisierbarkeit
        • Einleitung zu Diagonalisierbarkeit
        • Beispiel 1: Diagonalisierbarkeit
        • Beispiel 2: Diagonalisierbarkeit
        • Beispiel 3: Diagonalisierbarkeit
  • Vektorräume
    • Einleitung zu Vektorräume
    • Linearkombination von Vektoren
    • Lineare Abhängigkeit/Unabhängigkeit von Vektoren
      • Einleitung zu Lineare Abhängigkeit/Unabhängigkeit von Vektoren
      • Lineare Abhängigkeit im R²
      • Lineare Abhängigkeit im R³
    • Vektorraum, Erzeugendensystem, lineare Hülle, Basis
    • Vektorräume: Aufgaben und Lösungen
  • Komplexe Zahlen
    • Definition von komplexen Zahlen
    • Grundrechenarten der komplexen Zahlen
    • Komplexe Zahlen und Polarkoordinaten
    • Nullstellen von Polynomen
      • Einleitung zu Nullstellen von Polynomen
      • Fundamentalsatz der Algebra
      • abc- Formel (Mitternachtsformel) und pq-Formel
  • Elementare Funktionen
    • Einleitung zu Elementare Funktionen
    • Stetigkeit einer Funktion
    • Grenzwerte von Funktionen
    • Rationale Funktionen
      • Einleitung zu Rationale Funktionen
      • Ganzrationale Funktionen
        • Einleitung zu Ganzrationale Funktionen
        • Nullstellen ganzrationaler Funktionen
        • Grenzwerte ganzrationaler Funktionen
      • Gebrochenrationale Funktionen
        • Einleitung zu Gebrochenrationale Funktionen
        • Echt/unecht gebrochenrationale Funktion
        • Nullstellen und Definitionslücken gebrochenrationaler Funktionen
        • Hebbare Definitionslücke
        • Asymptoten
        • Grenzwerte gebrochenrationaler Funktionen
    • Nichtrationale Funktionen
      • Einleitung zu Nichtrationale Funktionen
      • Wurzelfunktionen
      • Exponentialfunktionen
        • Die allgemeine Exponentialfunktion
        • Die e-Funktion
      • Logarithmusfunktionen
      • Trigonometrische Funktionen
        • Einleitung zu Trigonometrische Funktionen
        • Das Bogenmaß und Eigenschaften der trigonomterischen Funktionen
        • Beziehungen trigonometrischer Funktionen
        • Rechenoperationen trigonometrischer Funktionen
          • Einleitung zu Rechenoperationen trigonometrischer Funktionen
          • Additionstheoreme trigonometrischer Funktionen
          • Summen und Differenzen trigonometrischer Funktionen
      • Hyperbelfunktionen
  • Differentialrechnung
    • Ableitungen
      • Einleitung zu Ableitungen
      • Ableitungen erster Ordnung
      • Ableitungen höherer Ordnung
    • Wendepunkte
    • Extremwerte
    • Ableitungsregeln
    • Ableitung der Elementaren Funktionen
    • Mittelwertsätze
    • Monotone Funktionen
    • Konkave und konvexe Funktionen
      • Einleitung zu Konkave und konvexe Funktionen
      • Nachweis Konkavität und Konvexität auf direktem Weg
      • Nachweis Konkavität und Konvexität durch Differentation
    • Regel von de l' Hospital
    • Näherungsverfahren zur Nullstellenberechnung nach Newton
  • Integralrechnung
    • Unbestimmte Integrale
      • Einleitung zu Unbestimmte Integrale
      • Rechenregeln für unbestimmte Integrale
      • Integration durch Substitution bei unbestimmten Integralen
      • Partielle Integration bei unbestimmten Integralen
      • Partialbruchzerlegung (rationale Zahlen) bei unbestimmten Integralen
      • Integration nicht-rationaler Zahlen bei unbestimmten Integralen
    • Bestimmte Integrale
      • Einleitung zu Bestimmte Integrale
      • Hauptsatz der Differential - und Integralrechnung
      • Integration durch Substitution bei bestimmten Integralen
      • Partielle Integration bei bestimmten Integralen
    • Uneigentliche Integrale
      • Einleitung zu Uneigentliche Integrale
      • Uneigentliche Integrale Typ 1
      • Uneigentliche Integrale Typ 2
  • Formelsammlung
    • Einleitung zu Formelsammlung
  • 128
  • 22
  • 214
  • 171
einmalig 39,00 €
Zur Kasse
Online-Kurs Top AngebotTrusted Shop
Abonnement

Dein Vollzugriff auf ingenieurkurse.de

Mache ingenieurkurse.de zu deinem Begleiter in deinem Studium oder deiner Aus- und Weiterbildung.
  Vollzugriff auf alle Online-Kurse
sowie alle zukünftigen Erweiterungen und laufende Aktualisierungen
  Alle Lernmaterialien komplett
mit mehr als 150 Videos, 1.480 interaktiven Übungsaufgaben und 1.500 Lerntexten
  Günstiger als bei Einzelbuchung
nur 14,90 € monatlich bei 12 Monaten Mindestvertragslaufzeit

JETZT BUCHEN
für 14,90 € monatlich

Empfehlung: