Analysis und Lineare Algebra
-
Einführung in die Vektorrechnung
Vektorrechnung > Einführung in die Vektorrechnung
 Unter Vektoren versteht man Objekte mit einer vorgegebenen Länge und Richtung. Mit Hilfe von Vektoren kann man z. B. die Geschwindigkeit von Objekten oder die Strömungsrichtungen in einem Raum darstellen. Vektoren werden durch ihre Koordinaten bestimmt. Ein Vektor in einem 2-dimensionalen Raum $\mathbb{R}^2$ besitzt dabei zwei Koordinaten, ein Vektor in einem 3-dimensionalen Raum $\mathbb{R}^3$ drei Koordinaten und ein Vektor in einem n-dimensionalen $\mathbb{R}^n$ Raum $n$ Koordinaten. Vektor ...
Unter Vektoren versteht man Objekte mit einer vorgegebenen Länge und Richtung. Mit Hilfe von Vektoren kann man z. B. die Geschwindigkeit von Objekten oder die Strömungsrichtungen in einem Raum darstellen. Vektoren werden durch ihre Koordinaten bestimmt. Ein Vektor in einem 2-dimensionalen Raum $\mathbb{R}^2$ besitzt dabei zwei Koordinaten, ein Vektor in einem 3-dimensionalen Raum $\mathbb{R}^3$ drei Koordinaten und ein Vektor in einem n-dimensionalen $\mathbb{R}^n$ Raum $n$ Koordinaten. Vektor ... -
Subtraktion von Vektoren
Vektorrechnung > Einführung in die Vektorrechnung > Subtraktion von Vektoren
 Die Subtraktion von zwei Vektoren $\vec{a} = \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right)$ und $\vec{b} = \left( \begin{array}{c} x_2 \\ y_2 \end{array} \right)$ ist definiert durch:$\vec{a} - \vec{b} := \left( \begin{array}{c} x_1 - x_2 \\ y_1 - y_2 \end{array} \right)$Die grafische Subtraktion des Vektors $\vec{b}$ vom Vektor $\vec{a}$ erfolgt, indem man den entgegengesetzten Vektor $- \vec{b}$ zum Vektor $\vec{a}$ hinzuaddiert. Man tauscht also ...
Die Subtraktion von zwei Vektoren $\vec{a} = \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right)$ und $\vec{b} = \left( \begin{array}{c} x_2 \\ y_2 \end{array} \right)$ ist definiert durch:$\vec{a} - \vec{b} := \left( \begin{array}{c} x_1 - x_2 \\ y_1 - y_2 \end{array} \right)$Die grafische Subtraktion des Vektors $\vec{b}$ vom Vektor $\vec{a}$ erfolgt, indem man den entgegengesetzten Vektor $- \vec{b}$ zum Vektor $\vec{a}$ hinzuaddiert. Man tauscht also ... -
Addition von Vektoren
Vektorrechnung > Einführung in die Vektorrechnung > Addition von Vektoren
 Die Addition von zwei Vektoren $\vec{a} = \left(\begin{array}{c} x_1 \\ y_1 \end{array} \right)$ und $\vec{b} = \left(\begin{array}{c} x_2 \\ y_2 \end{array} \right)$ ist definiert durch:$\vec{a} + \vec{b} := \left( \begin{array}{c} x_1 + x_2 \\ y_1 + y_2 \end{array} \right)$Die grafische Addition von Vektoren erfolgt, indem der Anfangspunkt des Vektors $\vec{b}$ an den Endpunkt des Vektors $\vec{a}$ angreiht wird. Dabei darf die Richtung der Vektoren nicht verändert werden. Der resultierende ...
Die Addition von zwei Vektoren $\vec{a} = \left(\begin{array}{c} x_1 \\ y_1 \end{array} \right)$ und $\vec{b} = \left(\begin{array}{c} x_2 \\ y_2 \end{array} \right)$ ist definiert durch:$\vec{a} + \vec{b} := \left( \begin{array}{c} x_1 + x_2 \\ y_1 + y_2 \end{array} \right)$Die grafische Addition von Vektoren erfolgt, indem der Anfangspunkt des Vektors $\vec{b}$ an den Endpunkt des Vektors $\vec{a}$ angreiht wird. Dabei darf die Richtung der Vektoren nicht verändert werden. Der resultierende ... -
Vektorraum, Erzeugendensystem, lineare Hülle, Basis
Vektorräume > Vektorraum, Erzeugendensystem, lineare Hülle, Basis
 Definition: VektorraumDie Elemente eines Vektorraums $\mathcal V$ heißen Vektoren. Sie können addiert oder mit Skalaren multipliziert werden. Das Ergebnis ist wieder ein Vektor desselben Vektorraums $\mathcal V$.Addition von VektorenEine Bedingung ist, dass die Vektoren miteinander addiert werden können. Sind also $\vec{a_1}, \vec{a_2}, ... , \vec{a_n}$ Vektoren aus $\mathcal V$, also $\vec{a_1}, \vec{a_2}, ... , \vec{a_n} \in \mathcal V$, dann muss es möglich sein, ihre ...
Definition: VektorraumDie Elemente eines Vektorraums $\mathcal V$ heißen Vektoren. Sie können addiert oder mit Skalaren multipliziert werden. Das Ergebnis ist wieder ein Vektor desselben Vektorraums $\mathcal V$.Addition von VektorenEine Bedingung ist, dass die Vektoren miteinander addiert werden können. Sind also $\vec{a_1}, \vec{a_2}, ... , \vec{a_n}$ Vektoren aus $\mathcal V$, also $\vec{a_1}, \vec{a_2}, ... , \vec{a_n} \in \mathcal V$, dann muss es möglich sein, ihre ... -
Lineare Abhängigkeit im R²
Vektorräume > Lineare Abhängigkeit/Unabhängigkeit von Vektoren > Lineare Abhängigkeit im R²
 Zwei Vektoren im R²Zwei Vektoren $\vec{a_1}$ und $\vec{a_2}$ sind genau dann linear abhängig, wenn sich der Nullvektor durch eine Linearkombination der Vektoren erzeugen lässt:$\lambda_1 \vec{a_1} + \lambda_2 \vec{a_2} = \vec{0}$mit$\lambda_1, \lambda_2 \in \mathbb{R}$Nehmen beide $\lambda_i$ den Wert null an, so sind die Vektoren voneinander unabhängig.Daraus folgt für die lineare Abhängigkeit, dass nicht beide $\lambda_i$ den Wert Null annehmen dürfen.Alternativ ...
Zwei Vektoren im R²Zwei Vektoren $\vec{a_1}$ und $\vec{a_2}$ sind genau dann linear abhängig, wenn sich der Nullvektor durch eine Linearkombination der Vektoren erzeugen lässt:$\lambda_1 \vec{a_1} + \lambda_2 \vec{a_2} = \vec{0}$mit$\lambda_1, \lambda_2 \in \mathbb{R}$Nehmen beide $\lambda_i$ den Wert null an, so sind die Vektoren voneinander unabhängig.Daraus folgt für die lineare Abhängigkeit, dass nicht beide $\lambda_i$ den Wert Null annehmen dürfen.Alternativ ... -
Lineare Abhängigkeit im R³
Vektorräume > Lineare Abhängigkeit/Unabhängigkeit von Vektoren > Lineare Abhängigkeit im R³
 Zwei Vektoren im R³Zwei Vektoren $\vec{a_1}$ und $\vec{a_2}$ sind genau dann linear abhängig, wenn sich der Nullvektor durch eine Linearkombination der Vektoren erzeugen lässt:$\lambda_1 \vec{a_1} + \lambda_2 \vec{a_2} = \vec{0}$mit$\lambda_1, \lambda_2 \in \mathbb{R}$Nehmen beide $\lambda_i$ den Wert null an, so sind die Vektoren voneinander unabhängig. Demnach gilt für die lineare Abhängigkeit, dass nicht beide $\lambda_i$ den Wert null annehmen dürfen.Sinnvoll ...
Zwei Vektoren im R³Zwei Vektoren $\vec{a_1}$ und $\vec{a_2}$ sind genau dann linear abhängig, wenn sich der Nullvektor durch eine Linearkombination der Vektoren erzeugen lässt:$\lambda_1 \vec{a_1} + \lambda_2 \vec{a_2} = \vec{0}$mit$\lambda_1, \lambda_2 \in \mathbb{R}$Nehmen beide $\lambda_i$ den Wert null an, so sind die Vektoren voneinander unabhängig. Demnach gilt für die lineare Abhängigkeit, dass nicht beide $\lambda_i$ den Wert null annehmen dürfen.Sinnvoll ... -
Lineare Abhängigkeit/Unabhängigkeit von Vektoren
Vektorräume > Lineare Abhängigkeit/Unabhängigkeit von Vektoren
 ... Unabhängigkeit von Vektoren beschäftigen. Lineare Abhängigkeit von VektorenDie Vektoren $\vec{a_1}$, $\vec{a_2}$, $...$, $\vec{a_n}$ heißen linear abhängig, wenn gilt: $\lambda_1 \vec{a_1} + \lambda_2 \vec{a_2} + ... + \lambda_n \vec{a_n} = \vec{0}$mit$\lambda_i \; (i = 1,2,...,n) \in \mathbb{R}$Dabei dürfen nicht alle $\lambda_i \; (i = 1,2,...,n)$ den Wert Null annehmen, damit die obige Gleichung erfüllt ist. Lässt ...
... Unabhängigkeit von Vektoren beschäftigen. Lineare Abhängigkeit von VektorenDie Vektoren $\vec{a_1}$, $\vec{a_2}$, $...$, $\vec{a_n}$ heißen linear abhängig, wenn gilt: $\lambda_1 \vec{a_1} + \lambda_2 \vec{a_2} + ... + \lambda_n \vec{a_n} = \vec{0}$mit$\lambda_i \; (i = 1,2,...,n) \in \mathbb{R}$Dabei dürfen nicht alle $\lambda_i \; (i = 1,2,...,n)$ den Wert Null annehmen, damit die obige Gleichung erfüllt ist. Lässt ... -
Einheitsvektor, Länge von Vektoren
Vektorrechnung > Einführung in die Vektorrechnung > Einheitsvektor, Länge von Vektoren
 Ein Vektor der die Länge $|1|$ besitzt, wird in der Mathematik als Einheitsvektor bezeichnet und weist in Richtung der positiven Koordinatenachsen.BasisvektorenDie drei Achsen $x$, $y$ und $z$ eines dreidimensionalen Koordinatensystems werden durch die drei Einheitsvektoren $\vec{e_1} = (1, 0, 0)$, $\vec{e_2} = (0, 1, 0)$ und $\vec{e_3} = (0, 0, 1)$ bestimmt. Da diese drei Vektoren die Basis für das Koordinatensystem bilden, werden diese speziellen Einheitsvektoren auch Basisvektoren ...
Ein Vektor der die Länge $|1|$ besitzt, wird in der Mathematik als Einheitsvektor bezeichnet und weist in Richtung der positiven Koordinatenachsen.BasisvektorenDie drei Achsen $x$, $y$ und $z$ eines dreidimensionalen Koordinatensystems werden durch die drei Einheitsvektoren $\vec{e_1} = (1, 0, 0)$, $\vec{e_2} = (0, 1, 0)$ und $\vec{e_3} = (0, 0, 1)$ bestimmt. Da diese drei Vektoren die Basis für das Koordinatensystem bilden, werden diese speziellen Einheitsvektoren auch Basisvektoren ... -
Übungsaufgaben zur Vektorrechnung
Vektorrechnung > Übungsaufgaben zur Vektorrechnung
 ... stellen wir einige Beispielaufgaben zur Vektorrechnung vor.Aufgabe 1: Addition und Subtraktion sowie Multiplikation mit einem SkalarGegeben seien die Vektoren $\vec{a} = (2,-4,1)$ und $\vec{b} = (1,1,-2)$.Bitte berechne:a) $\, \vec{a} + \vec{b}$b) $\, -2\vec{a}$c) $\, 3\vec{a} - 2\vec{b}$a) $\, \vec{a} + \vec{b} = (2+1, -4+1, 1-2) = (3, -3, -1) $b) $\, -2\vec{a} = -2((2,-4,1) = (-4,8,-2)$c) $\, 3\vec{a} - 2\vec{b} = 3(2,-4,1) - 2(1,1,-2) = (4,-14,7)$Aufgabe ...
... stellen wir einige Beispielaufgaben zur Vektorrechnung vor.Aufgabe 1: Addition und Subtraktion sowie Multiplikation mit einem SkalarGegeben seien die Vektoren $\vec{a} = (2,-4,1)$ und $\vec{b} = (1,1,-2)$.Bitte berechne:a) $\, \vec{a} + \vec{b}$b) $\, -2\vec{a}$c) $\, 3\vec{a} - 2\vec{b}$a) $\, \vec{a} + \vec{b} = (2+1, -4+1, 1-2) = (3, -3, -1) $b) $\, -2\vec{a} = -2((2,-4,1) = (-4,8,-2)$c) $\, 3\vec{a} - 2\vec{b} = 3(2,-4,1) - 2(1,1,-2) = (4,-14,7)$Aufgabe ... -
Zerlegung von Vektoren
Vektorrechnung > Das Skalarprodukt > Zerlegung von Vektoren
 Vektor Wie bereits in dem vorherigen Kapitel gezeigt, kann man mit dem Skalarprodukt den Winkel zwischen zwei Vektoren bestimmen.In diesem Abschnitt soll gezeigt werden, wie man einen Vektor $\vec{a}$ durch einen anderen Vektor $\vec{b}$ und einem zu $\vec{b}$ orthogonalen (senkrechten) Vektor $\vec{x}$ darstellt.Die orthogonale Zerlegung eines Vektors $\vec{a}$ bezüglich eines Vektors $\vec{b}$ (auch als orthogonale Projektion bezeichnet) ist die ...
Vektor Wie bereits in dem vorherigen Kapitel gezeigt, kann man mit dem Skalarprodukt den Winkel zwischen zwei Vektoren bestimmen.In diesem Abschnitt soll gezeigt werden, wie man einen Vektor $\vec{a}$ durch einen anderen Vektor $\vec{b}$ und einem zu $\vec{b}$ orthogonalen (senkrechten) Vektor $\vec{x}$ darstellt.Die orthogonale Zerlegung eines Vektors $\vec{a}$ bezüglich eines Vektors $\vec{b}$ (auch als orthogonale Projektion bezeichnet) ist die ...Skalieren von Vektoren
Vektorrechnung > Einführung in die Vektorrechnung > Skalieren von Vektoren
 Die Multiplikation eines Vektors mit einer Zahl nennt man Skalierung eines Vektors. Das Produkt ist wiederum ein Vektor, der entsprechend des mit ihm multiplizierten Werteslänger $\longrightarrow (2 \cdot \vec{a})$,kürzer $\longrightarrow (0,5 \cdot \vec{a})$ oder sogarin entgegengesetzter Richtung $\longrightarrow (-0,5 \cdot \vec{a})$neu abgebildet wird.Skalieren von Vektoren In der obigen Grafik ist deutlich zu erkennen, dass ein Vektor $\vec{a}$ multipliziert ...
Die Multiplikation eines Vektors mit einer Zahl nennt man Skalierung eines Vektors. Das Produkt ist wiederum ein Vektor, der entsprechend des mit ihm multiplizierten Werteslänger $\longrightarrow (2 \cdot \vec{a})$,kürzer $\longrightarrow (0,5 \cdot \vec{a})$ oder sogarin entgegengesetzter Richtung $\longrightarrow (-0,5 \cdot \vec{a})$neu abgebildet wird.Skalieren von Vektoren In der obigen Grafik ist deutlich zu erkennen, dass ein Vektor $\vec{a}$ multipliziert ...Linearkombination von Vektoren
Vektorräume > Linearkombination von Vektoren
 Die Linearkombination von Vektoren bezeichnet die Summe von Vektoren, wobei jeder Vektor mit einer reellen Zahl multipliziert wird. Das Ergebnis ist wieder ein Vektor.$\vec{v} = \lambda_1 \vec{a_1} + \lambda_2 \vec{a_2} + ... + \lambda_n \vec{a_n}$ Dabei sind $\vec{a_i}$ die Vektoren, $\lambda_i$ die reellen Zahlen und $\vec{v}$ der Ergebnisvektor.Der Vektor $\vec{v}$ ist eine Linearkombination aus den obigen Vektoren $\vec{a_i}$.Darstellung eines Vektors als Linearkombination Wir wollen ...
Die Linearkombination von Vektoren bezeichnet die Summe von Vektoren, wobei jeder Vektor mit einer reellen Zahl multipliziert wird. Das Ergebnis ist wieder ein Vektor.$\vec{v} = \lambda_1 \vec{a_1} + \lambda_2 \vec{a_2} + ... + \lambda_n \vec{a_n}$ Dabei sind $\vec{a_i}$ die Vektoren, $\lambda_i$ die reellen Zahlen und $\vec{v}$ der Ergebnisvektor.Der Vektor $\vec{v}$ ist eine Linearkombination aus den obigen Vektoren $\vec{a_i}$.Darstellung eines Vektors als Linearkombination Wir wollen ...Skalarprodukt und Winkel
Vektorrechnung > Das Skalarprodukt > Skalarprodukt und Winkel
 Sind zwei Vektoren $\vec{a} \neq 0$ und $\vec{b} \neq 0$ (also vom Nullvektor verschieden), so existiert ein Winkel $\varphi$, welcher von $\vec{a}$ und $\vec{b}$ eingeschlossen wird mit $0 \le \varphi \le \pi$.eingeschlossener WinkelSkalarproduktDas Skalarprodukt zweier Vektoren $\vec{a}$ und $\vec{b}$ ergibt eine Zahl (Skalar).Für die Berechnung des Skalarprodukts im kartesischen Koordinatensystem verwendet man folgende Formel, bei der der Winkel zwischen den beiden Vektoren nicht ...
Sind zwei Vektoren $\vec{a} \neq 0$ und $\vec{b} \neq 0$ (also vom Nullvektor verschieden), so existiert ein Winkel $\varphi$, welcher von $\vec{a}$ und $\vec{b}$ eingeschlossen wird mit $0 \le \varphi \le \pi$.eingeschlossener WinkelSkalarproduktDas Skalarprodukt zweier Vektoren $\vec{a}$ und $\vec{b}$ ergibt eine Zahl (Skalar).Für die Berechnung des Skalarprodukts im kartesischen Koordinatensystem verwendet man folgende Formel, bei der der Winkel zwischen den beiden Vektoren nicht ...Das Vektorprodukt
Vektorrechnung > Das Vektorprodukt
 Das Vektorprodukt (auch Kreuzprodukt) ist anders als das Skalarprodukt ein Vektor und keine Zahl. Gekennzeichnet wird es durch $\times$ statt durch das Multiplikationszeichen $\cdot$ (siehe Skalarprodukt). Bei der Schreibweise $\vec{a} \times \vec{b}$ ergibt sich also ein Vektor als Ergebnis, wohingegen bei der Schreibweise $\vec{a} \cdot \vec{b}$ eine Zahl das Ergebnis ist.Eigenschaften des VektorproduktsDas Vektorprodukt $\vec{a} \times \vec{b}$ aus den beiden Vektoren $\vec{a}$ und $\vec{b}$ ...
Das Vektorprodukt (auch Kreuzprodukt) ist anders als das Skalarprodukt ein Vektor und keine Zahl. Gekennzeichnet wird es durch $\times$ statt durch das Multiplikationszeichen $\cdot$ (siehe Skalarprodukt). Bei der Schreibweise $\vec{a} \times \vec{b}$ ergibt sich also ein Vektor als Ergebnis, wohingegen bei der Schreibweise $\vec{a} \cdot \vec{b}$ eine Zahl das Ergebnis ist.Eigenschaften des VektorproduktsDas Vektorprodukt $\vec{a} \times \vec{b}$ aus den beiden Vektoren $\vec{a}$ und $\vec{b}$ ...Vektorräume: Aufgaben und Lösungen
Vektorräume > Vektorräume: Aufgaben und Lösungen
 Aufgabe 1: Untervektorraum$\vec{V}= \{ \left( \begin{array}{c} 2 \\ a \end{array} \right) | a \in \mathbb{R} \}$ sei eine Teilmenge von $\mathbb{R}^2$.Überprüfe, ob $V$ einen Untervektorraum darstellt!Lösung: Es müssen 3 Bedingungen geprüft werden:Der Nullvektor muß im Unterraum enthalten seinDer Unterraum muss abgeschlossen bezüglich der Addition sein, d. h. wenn zwei Vektoren aus dem Unterraum addiert werden, dann ist die Summe auch ...
Aufgabe 1: Untervektorraum$\vec{V}= \{ \left( \begin{array}{c} 2 \\ a \end{array} \right) | a \in \mathbb{R} \}$ sei eine Teilmenge von $\mathbb{R}^2$.Überprüfe, ob $V$ einen Untervektorraum darstellt!Lösung: Es müssen 3 Bedingungen geprüft werden:Der Nullvektor muß im Unterraum enthalten seinDer Unterraum muss abgeschlossen bezüglich der Addition sein, d. h. wenn zwei Vektoren aus dem Unterraum addiert werden, dann ist die Summe auch ...Dreiecksungleichung
Vektorrechnung > Einführung in die Vektorrechnung > Dreiecksungleichung
 ... b$|a + b|$ = Länge der Seite a+bFür Vektoren gilt analog: Dreiecksungleichung für Vektoren: $|\vec{a}| + |\vec{b}| \ge |\vec{a} + \vec{b}|$mit$|\vec{a}| $ = Länge der Seite a$|\vec{b}|$ = Länge der Seite b$|\vec{a} + \vec{b}|$ = Länge der Seite a+bBeweis der DreiecksungleichungDer Beweis der Dreiecksungleichung wird wie folgt durchgeführt:Es gilt:Wenn $a \le |a|$ und $b \le |b| \;\;\;\;\; \longrightarrow$ (1) ...
... b$|a + b|$ = Länge der Seite a+bFür Vektoren gilt analog: Dreiecksungleichung für Vektoren: $|\vec{a}| + |\vec{b}| \ge |\vec{a} + \vec{b}|$mit$|\vec{a}| $ = Länge der Seite a$|\vec{b}|$ = Länge der Seite b$|\vec{a} + \vec{b}|$ = Länge der Seite a+bBeweis der DreiecksungleichungDer Beweis der Dreiecksungleichung wird wie folgt durchgeführt:Es gilt:Wenn $a \le |a|$ und $b \le |b| \;\;\;\;\; \longrightarrow$ (1) ...Formelsammlung
Formelsammlung
 ... Möglichkeiten 6 "Richtige" zu ziehen.2. VektorrechnungOrtsvektoren beginnen immer im Ursprung $(0,0)$ und zeigen auf einen bestimmten Punkt. Z.B. beginnt der Vektor $\vec{a} = (4,3)$ im Ursprung und zeigt auf den Punkt $A(4,3)$.Addition von Vektoren$\vec{a} + \vec{b} = (a_1 + b_1, a_2 + b_2, a_3 + b_3)$Subtraktion von Vektoren $\vec{a} - \vec{b} = (a_1 - b_1, a_2 - b_2, a_3 - b_3)$Skalieren eines Vektors $\vec{a}$ $s \cdot \vec{a}$$s > 0$ Vektor wird länger$0 < ...
... Möglichkeiten 6 "Richtige" zu ziehen.2. VektorrechnungOrtsvektoren beginnen immer im Ursprung $(0,0)$ und zeigen auf einen bestimmten Punkt. Z.B. beginnt der Vektor $\vec{a} = (4,3)$ im Ursprung und zeigt auf den Punkt $A(4,3)$.Addition von Vektoren$\vec{a} + \vec{b} = (a_1 + b_1, a_2 + b_2, a_3 + b_3)$Subtraktion von Vektoren $\vec{a} - \vec{b} = (a_1 - b_1, a_2 - b_2, a_3 - b_3)$Skalieren eines Vektors $\vec{a}$ $s \cdot \vec{a}$$s > 0$ Vektor wird länger$0 < ...Das Spatprodukt
Vektorrechnung > Das Spatprodukt
 ... stellt eine Kombination aus Skalar- und Vektorprodukt dar. Es wird aus je drei Vektoren gebildet. Schreibweise: [$\vec{a},\vec{b},\vec{c}] :=\vec{a} \cdot (\vec{b}$ x $\vec{c}):=\vec{b} \cdot (\vec{a}$ x $\vec{c}):=\vec{c} \cdot (\vec{a}$ x $\vec{b})$.Der von den Vektoren aufgespannte Spat hat das Volumen $V = |[\vec{a},\vec{b},\vec{c}]|$.Im Umkehrschluss bedeutet dies:1. Liegen alle 3 Vektoren in einer Ebene, so ergibt ihr Spatprodukt null:$\;\;\;[\vec{a},\vec{b},\vec{c}] = 0$2. ...
... stellt eine Kombination aus Skalar- und Vektorprodukt dar. Es wird aus je drei Vektoren gebildet. Schreibweise: [$\vec{a},\vec{b},\vec{c}] :=\vec{a} \cdot (\vec{b}$ x $\vec{c}):=\vec{b} \cdot (\vec{a}$ x $\vec{c}):=\vec{c} \cdot (\vec{a}$ x $\vec{b})$.Der von den Vektoren aufgespannte Spat hat das Volumen $V = |[\vec{a},\vec{b},\vec{c}]|$.Im Umkehrschluss bedeutet dies:1. Liegen alle 3 Vektoren in einer Ebene, so ergibt ihr Spatprodukt null:$\;\;\;[\vec{a},\vec{b},\vec{c}] = 0$2. ...Komplexe Zahlen und Polarkoordinaten
Komplexe Zahlen > Komplexe Zahlen und Polarkoordinaten
 ... Punktes ermitteln. Dabei ist $\vec{r}$ der Vektor, der auf den Punkt zeigt und $r = |\vec{r}|$ ist die Länge des Vektors. Dieser Zusammhang wurde bereits im Kapitel Vektorrechnung behandelt. Ist der Vektor $\vec{r} \neq (0,0)$ (also vom Nullvektor verschieden), dann ist die Länge des Vektor größer null: $r > 0$. Wie du in der folgenden Grafik siehst, existiert dann ein Winkel $\varphi$, welcher sich mit der positiven x-Achse (Polarwinkel) bilden lässt.PolarkoordinatenUmformung ...
... Punktes ermitteln. Dabei ist $\vec{r}$ der Vektor, der auf den Punkt zeigt und $r = |\vec{r}|$ ist die Länge des Vektors. Dieser Zusammhang wurde bereits im Kapitel Vektorrechnung behandelt. Ist der Vektor $\vec{r} \neq (0,0)$ (also vom Nullvektor verschieden), dann ist die Länge des Vektor größer null: $r > 0$. Wie du in der folgenden Grafik siehst, existiert dann ein Winkel $\varphi$, welcher sich mit der positiven x-Achse (Polarwinkel) bilden lässt.PolarkoordinatenUmformung ...Identische Geraden
Vektorrechnung > Geraden im Raum > Identische Geraden
 ... für identische Geraden:1. Die Richtungsvektoren $\vec{v}$ und $\vec{u}$ sind Vielfache voneinander (kollinear).2. Der Stützvektor der einen Geraden befindet sich auf der anderen Geraden.Sind beide Bedingungen erfüllt, so handelt es sich um identische Geraden.Sind beide Bedingungen erfüllt, so handelt es sich um identische Geraden.Der Stützvektor ist dabei der Ortsvektor eines beliebigen Punkts auf der Geraden. Dieser wird auch als Aufpunkt bezeichnet. So ist ...
... für identische Geraden:1. Die Richtungsvektoren $\vec{v}$ und $\vec{u}$ sind Vielfache voneinander (kollinear).2. Der Stützvektor der einen Geraden befindet sich auf der anderen Geraden.Sind beide Bedingungen erfüllt, so handelt es sich um identische Geraden.Sind beide Bedingungen erfüllt, so handelt es sich um identische Geraden.Der Stützvektor ist dabei der Ortsvektor eines beliebigen Punkts auf der Geraden. Dieser wird auch als Aufpunkt bezeichnet. So ist ...Übungsaufgaben zu Geraden im Raum
Vektorrechnung > Geraden im Raum > Übungsaufgaben zu Geraden im Raum
 ... sind. Dazu betrachten wir die Richtungsvektoren der beiden Geraden und berechnen $\lambda$:$\vec{v} = \lambda \; \vec{w}$ (alternativ: $\vec{w} = \lambda \vec{v}$).$\left(\begin{array}{c} 1 \\ 2 \\ -2 \end{array}\right) = \lambda \left(\begin{array}{c} 3 \\ 1 \\ -3 \end{array}\right)$Wir stellen das lineare Gleichungssystem auf:(1) $1 = 3\lambda $(2) $2 = \lambda$(3) $-2 = -3\lambda$Jede Zeile nach $\lambda$ auflösen:(1) $\lambda = \frac{1}{3}$(2) ...
... sind. Dazu betrachten wir die Richtungsvektoren der beiden Geraden und berechnen $\lambda$:$\vec{v} = \lambda \; \vec{w}$ (alternativ: $\vec{w} = \lambda \vec{v}$).$\left(\begin{array}{c} 1 \\ 2 \\ -2 \end{array}\right) = \lambda \left(\begin{array}{c} 3 \\ 1 \\ -3 \end{array}\right)$Wir stellen das lineare Gleichungssystem auf:(1) $1 = 3\lambda $(2) $2 = \lambda$(3) $-2 = -3\lambda$Jede Zeile nach $\lambda$ auflösen:(1) $\lambda = \frac{1}{3}$(2) ...Geraden im Raum
Vektorrechnung > Geraden im Raum
 ... können mittels Parameterdarstellung durch Vektoren abgebildet werden. Gerade durch den UrsprungEine Gerade durch den Koordinatenursprung wird allgemein definiert als:$G: \vec{x} = t \cdot \vec{v}$ mit$t \in \mathbb{R}$ = Parameter$\vec{v}$ = RichtungsvektorDie Gerade mit obiger Gleichung verläuft dabei durch den Nullpunkt. Der Richtungsvektor $\vec{v}$ zeigt dabei die Richtung der Geraden an, der Parameter $t$ die Länge der Geraden. In der folgenden Grafik ist der Richtungsvektor ...
... können mittels Parameterdarstellung durch Vektoren abgebildet werden. Gerade durch den UrsprungEine Gerade durch den Koordinatenursprung wird allgemein definiert als:$G: \vec{x} = t \cdot \vec{v}$ mit$t \in \mathbb{R}$ = Parameter$\vec{v}$ = RichtungsvektorDie Gerade mit obiger Gleichung verläuft dabei durch den Nullpunkt. Der Richtungsvektor $\vec{v}$ zeigt dabei die Richtung der Geraden an, der Parameter $t$ die Länge der Geraden. In der folgenden Grafik ist der Richtungsvektor ...Cramersche Regel
Matrizen > Determinanten > Cramersche Regel
 ... -8 \\ -2 & 6 & 7 \end{pmatrix}$ und der Vektor $\vec{b} = \begin{pmatrix} 2 \\ 4 \\ -1 \end{pmatrix}$.Berechnung der Determinanten $|A| = \begin{vmatrix} -1 & 2 & 4 \\ 2 & 5 & -8 \\ -2 & 6 & 7 \end{vmatrix}$Regel von Sarrus$|A| = -1 \cdot 5 \cdot 7 + 2 \cdot 6 \cdot 4 + (-2) \cdot 2 \cdot (-8) - 4 \cdot 5 \cdot (-2) - (-8) \cdot 6 \cdot (-1) - 7 \cdot 2 \cdot 2 = 9$Da $|A| \neq 0$ besitzt das Gleichungssystem eine eindeutige Lösung, welche ...
... -8 \\ -2 & 6 & 7 \end{pmatrix}$ und der Vektor $\vec{b} = \begin{pmatrix} 2 \\ 4 \\ -1 \end{pmatrix}$.Berechnung der Determinanten $|A| = \begin{vmatrix} -1 & 2 & 4 \\ 2 & 5 & -8 \\ -2 & 6 & 7 \end{vmatrix}$Regel von Sarrus$|A| = -1 \cdot 5 \cdot 7 + 2 \cdot 6 \cdot 4 + (-2) \cdot 2 \cdot (-8) - 4 \cdot 5 \cdot (-2) - (-8) \cdot 6 \cdot (-1) - 7 \cdot 2 \cdot 2 = 9$Da $|A| \neq 0$ besitzt das Gleichungssystem eine eindeutige Lösung, welche ...Eigenvektoren
Matrizen > Eigenwerte und Eigenvektoren > Eigenvektoren
 ... Kurstext zeigen wir dir die Berechnung der Eigenvektoren zu verschiedenen Eigenwerten.Der zu dem Eigenwert $\lambda$ gehörende Eigenvektor $\vec{x}$ ist die Lösung der Gleichung$(A - \lambda E)\vec{x} = 0$, wobei $\vec{x} \neq \vec{0}$ gilt. AnwendungsbeispielGegeben sei die Matrix aus dem vorherigen Beispiel $A = \begin{pmatrix} 3 & 0 \\ -4 & 5 \end{pmatrix}$ mit den Eigenwerten $\lambda_1 = 5, \lambda_2 = 3$. Berechne die zugehörigen Eigenvektoren zu $\lambda_1$ ...
... Kurstext zeigen wir dir die Berechnung der Eigenvektoren zu verschiedenen Eigenwerten.Der zu dem Eigenwert $\lambda$ gehörende Eigenvektor $\vec{x}$ ist die Lösung der Gleichung$(A - \lambda E)\vec{x} = 0$, wobei $\vec{x} \neq \vec{0}$ gilt. AnwendungsbeispielGegeben sei die Matrix aus dem vorherigen Beispiel $A = \begin{pmatrix} 3 & 0 \\ -4 & 5 \end{pmatrix}$ mit den Eigenwerten $\lambda_1 = 5, \lambda_2 = 3$. Berechne die zugehörigen Eigenvektoren zu $\lambda_1$ ...einmalig 39,00 Euro / kein Abo
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Physik
-
Vektoraddition
Mathematische Grundlagen > Vektoren, Ortsvektoren und Richtungsvektoren > Vektoraddition
 Die Addition von Vektoren ist Gegenstand dieses Abschnittes. Sind zwei Vektoren $\vec{a}$ und $\vec{b}$ gegeben, so bestimmt sich die Addition der beiden Vektoren wie folgt:Addition: $\vec{a} + \vec{b} = \left( \begin{array}{c} a_x + b_x \\ a_y + b_y \\ a_z + b_z \\ ... \\ a_n + b_n \end{array} \right)$Bei der Addition von Vektoren werden die einzelnen $x$-,$y$- und $z$-Werte der einzelnen Vektoren miteinander addiert.Die Vekoraddition ist kommutativ, d.h. die Reihenfolge in welcher die Vektoren ...
Die Addition von Vektoren ist Gegenstand dieses Abschnittes. Sind zwei Vektoren $\vec{a}$ und $\vec{b}$ gegeben, so bestimmt sich die Addition der beiden Vektoren wie folgt:Addition: $\vec{a} + \vec{b} = \left( \begin{array}{c} a_x + b_x \\ a_y + b_y \\ a_z + b_z \\ ... \\ a_n + b_n \end{array} \right)$Bei der Addition von Vektoren werden die einzelnen $x$-,$y$- und $z$-Werte der einzelnen Vektoren miteinander addiert.Die Vekoraddition ist kommutativ, d.h. die Reihenfolge in welcher die Vektoren ... -
Vektorsubtraktion
Mathematische Grundlagen > Vektoren, Ortsvektoren und Richtungsvektoren > Vektorsubtraktion
 Die Subtraktion von Vektoren ist Gegenstand dieses Abschnittes. Sind zwei Vektoren $\vec{a}$ und $\vec{b}$ gegeben, so bestimmt sich die Subtraktion der beiden Vektoren wie folgt:Subtraktion: $\vec{a} - \vec{b} = \left( \begin{array}{c} a_x - b_x \\ a_y - b_y \\ a_z - b_z \\ ... \\ a_n - b_n \end{array} \right)$Bei der Subtraktion von Vektoren werden die einzelnen $x$-,$y$- und $z$-Werte der jeweiligen Vektoren voneinander subtrahiert.Im Gegensatz zur Vektoraddition ist die Vektorsubtraktion ...
Die Subtraktion von Vektoren ist Gegenstand dieses Abschnittes. Sind zwei Vektoren $\vec{a}$ und $\vec{b}$ gegeben, so bestimmt sich die Subtraktion der beiden Vektoren wie folgt:Subtraktion: $\vec{a} - \vec{b} = \left( \begin{array}{c} a_x - b_x \\ a_y - b_y \\ a_z - b_z \\ ... \\ a_n - b_n \end{array} \right)$Bei der Subtraktion von Vektoren werden die einzelnen $x$-,$y$- und $z$-Werte der jeweiligen Vektoren voneinander subtrahiert.Im Gegensatz zur Vektoraddition ist die Vektorsubtraktion ... -
Skalarprodukt
Mathematische Grundlagen > Vektoren, Ortsvektoren und Richtungsvektoren > Skalarprodukt
 Sind zwei Vektoren $\vec{a} \neq 0$ und $\vec{b} \neq 0$ (also vom Nullvektor verschieden), so existiert ein Winkel $\varphi$, welcher von $\vec{a}$ und $\vec{b}$ eingeschlossen wird mit $0 \le \varphi \le \pi$.Unterschiedliche Winkel, SkalarproduktIn der obigen Grafik sind je zwei Vektoren gegeben mit einem eingeschlossenen Winkel $\varphi$. Links ist ein spitzer Winkel veranschaulicht, welcher durch ein positives Skalarprodukt angezeigt wird, der stumpfe Winkel rechts wird durch ein negatives ...
Sind zwei Vektoren $\vec{a} \neq 0$ und $\vec{b} \neq 0$ (also vom Nullvektor verschieden), so existiert ein Winkel $\varphi$, welcher von $\vec{a}$ und $\vec{b}$ eingeschlossen wird mit $0 \le \varphi \le \pi$.Unterschiedliche Winkel, SkalarproduktIn der obigen Grafik sind je zwei Vektoren gegeben mit einem eingeschlossenen Winkel $\varphi$. Links ist ein spitzer Winkel veranschaulicht, welcher durch ein positives Skalarprodukt angezeigt wird, der stumpfe Winkel rechts wird durch ein negatives ... -
Länge von Vektoren
Mathematische Grundlagen > Vektoren, Ortsvektoren und Richtungsvektoren > Länge von Vektoren
 ... wir uns mit der Länge eines Vektors. Die Länge eines Vektors wird in der Mathematik Betrag des Vektors genannt und mit Betragsstrichen gekennzeichnet:$|\vec{a}|$ Länge des Vektors $\vec{a}$Der Betrag eines Vektors ist eine skalare Größe und immer positiv, außer es handelt sich um einen Nullvektor (Betrag gleich Null).Die Länge eines Vektors $\vec{a} \in \mathbb{R}^n $ kann bestimmt werden ...
... wir uns mit der Länge eines Vektors. Die Länge eines Vektors wird in der Mathematik Betrag des Vektors genannt und mit Betragsstrichen gekennzeichnet:$|\vec{a}|$ Länge des Vektors $\vec{a}$Der Betrag eines Vektors ist eine skalare Größe und immer positiv, außer es handelt sich um einen Nullvektor (Betrag gleich Null).Die Länge eines Vektors $\vec{a} \in \mathbb{R}^n $ kann bestimmt werden ... -
Vektoren, Ortsvektoren und Richtungsvektoren
Mathematische Grundlagen > Vektoren, Ortsvektoren und Richtungsvektoren
 ... Diese Größen werden dann als Vektoren dargestellt. Die folgenden Abschnitte behandeln den Umgang mit Vektoren. Wir betrachten in diesem Zusammenhang:Vektoraddition und -subtraktion,Länge von VektorenSkalarprodukt/Vektorprodukt SpatproduktDefinition: VektorenUnter Vektoren versteht man Objekte mit einer vorgegebenen Länge und Richtung. Mit Hilfe von Vektoren kann man z.B. die Geschwindigkeit von Objekten oder die Strömungsrichtungen in einem Raum darstellen. ...
... Diese Größen werden dann als Vektoren dargestellt. Die folgenden Abschnitte behandeln den Umgang mit Vektoren. Wir betrachten in diesem Zusammenhang:Vektoraddition und -subtraktion,Länge von VektorenSkalarprodukt/Vektorprodukt SpatproduktDefinition: VektorenUnter Vektoren versteht man Objekte mit einer vorgegebenen Länge und Richtung. Mit Hilfe von Vektoren kann man z.B. die Geschwindigkeit von Objekten oder die Strömungsrichtungen in einem Raum darstellen. ... -
Vektorprodukt
Mathematische Grundlagen > Vektoren, Ortsvektoren und Richtungsvektoren > Vektorprodukt
 Das Vektorprodukt ist anders als das Skalarprodukt ein Vektor und keine Zahl. Gekennzeichnet wird es durch $\times$ statt durch das Multiplikationszeichen $\cdot$. Bei der Schreibweise $\vec{a} \times \vec{b}$ ergibt sich also ein Vektor als Ergebnis, wo hingegen bei der Schreibweise $\vec{a} \cdot \vec{b}$ eine Zahl das Ergebnis ist.Das Vektorprodukt aus zwei Vektoren $\vec{a}$ und $\vec{b}$ kann wie folgt berechnet werden:$\vec{a} \times \vec{b} = \left( \begin{array}{c} a_1 \\ a_2 ...
Das Vektorprodukt ist anders als das Skalarprodukt ein Vektor und keine Zahl. Gekennzeichnet wird es durch $\times$ statt durch das Multiplikationszeichen $\cdot$. Bei der Schreibweise $\vec{a} \times \vec{b}$ ergibt sich also ein Vektor als Ergebnis, wo hingegen bei der Schreibweise $\vec{a} \cdot \vec{b}$ eine Zahl das Ergebnis ist.Das Vektorprodukt aus zwei Vektoren $\vec{a}$ und $\vec{b}$ kann wie folgt berechnet werden:$\vec{a} \times \vec{b} = \left( \begin{array}{c} a_1 \\ a_2 ... -
Skalare und Vektoren
Mathematische Grundlagen > Skalare und Vektoren
 ... Skalar, liegt der letztere Fall vor von einem Vektor.Ein Skalar ist eine physikalische Größe, die durch die Angabe eines Zahlenwertes und ihrer Einheit charakterisiert ist. Betrachten wir zunächst einige Beispiele für Skalare:Ein typisches Beispiel für einen Skalar in der Physik ist die Temperatur. Das Thermometer zeigt an einem warmen Sommertag beispielsweise eine Temperatur von $t = 30°$ an. Die Angabe der Temperatur besteht aus einem Zahlenwert ...
... Skalar, liegt der letztere Fall vor von einem Vektor.Ein Skalar ist eine physikalische Größe, die durch die Angabe eines Zahlenwertes und ihrer Einheit charakterisiert ist. Betrachten wir zunächst einige Beispiele für Skalare:Ein typisches Beispiel für einen Skalar in der Physik ist die Temperatur. Das Thermometer zeigt an einem warmen Sommertag beispielsweise eine Temperatur von $t = 30°$ an. Die Angabe der Temperatur besteht aus einem Zahlenwert ... -
Spatprodukt
Mathematische Grundlagen > Vektoren, Ortsvektoren und Richtungsvektoren > Spatprodukt
 ... Das Spatprodukt ist eine Kombination aus dem Vektorprodukt und dem Skalarprodukt und wird aus drei Vektoren gebildet:[$\vec{a},\vec{b},\vec{c}] :=\vec{a} \cdot (\vec{b}$ x $\vec{c}):=\vec{b} \cdot (\vec{a}$ x $\vec{c}):=\vec{c} \cdot (\vec{a}$ x $\vec{b})$.Der von den Vektoren aufgespannte Spat hat das Volumen $V = |[\vec{a},\vec{b},\vec{c}]|$.Im Umkehrschluss bedeutet dies:Liegen alle 3 Vektoren in einer Ebene so verschwindet das Spatprodukt, also $[\vec{a},\vec{b},\vec{c}] ...
... Das Spatprodukt ist eine Kombination aus dem Vektorprodukt und dem Skalarprodukt und wird aus drei Vektoren gebildet:[$\vec{a},\vec{b},\vec{c}] :=\vec{a} \cdot (\vec{b}$ x $\vec{c}):=\vec{b} \cdot (\vec{a}$ x $\vec{c}):=\vec{c} \cdot (\vec{a}$ x $\vec{b})$.Der von den Vektoren aufgespannte Spat hat das Volumen $V = |[\vec{a},\vec{b},\vec{c}]|$.Im Umkehrschluss bedeutet dies:Liegen alle 3 Vektoren in einer Ebene so verschwindet das Spatprodukt, also $[\vec{a},\vec{b},\vec{c}] ... -
Drehmoment
Kinetik: Ursache von Bewegungen > Drehmoment
 ... senkrechter Abstand (Hebelarm)$F$ KraftIn vektorieller Schreibweise muss das Vektorprodukt gebildet werden:$\vec{M} = \vec{F} \cdot \vec{s}$Es handelt sich hierbei also um das Vektorprodukt (auch Kreuzprodukt) aus Kraft $\vec{F}$ und senkrechtem Abstand $\vec{s}$. Dabei ist der resultierende Vektor $\vec{M}$ das Drehmoment. Zur Erinnerung: Das Kreuzprodukt der Vektoren $\vec{a}$ und $\vec{b}$ ist ein Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene ...
... senkrechter Abstand (Hebelarm)$F$ KraftIn vektorieller Schreibweise muss das Vektorprodukt gebildet werden:$\vec{M} = \vec{F} \cdot \vec{s}$Es handelt sich hierbei also um das Vektorprodukt (auch Kreuzprodukt) aus Kraft $\vec{F}$ und senkrechtem Abstand $\vec{s}$. Dabei ist der resultierende Vektor $\vec{M}$ das Drehmoment. Zur Erinnerung: Das Kreuzprodukt der Vektoren $\vec{a}$ und $\vec{b}$ ist ein Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene ... -
Zerlegung von Vektoren
Mathematische Grundlagen > Vektoren, Ortsvektoren und Richtungsvektoren > Zerlegung von Vektoren
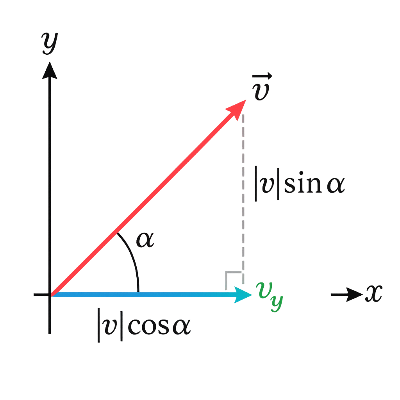 Vektorzerlegung bedeutet, einen Vektor in „einfache“ Richtungsanteile zu zerlegen – typischerweise entlang von Achsen (x, y, z) oder entlang irgendeiner gewünschten Richtung. Anschaulich: Stell dir eine Pfeilspitze vor, deren „Schatten“ auf ausgewählten Richtungen wir getrennt betrachten.---1) Zerlegung entlang kartesischer AchsenIn 2D:$\vec v =\begin{pmatrix} v_x \\ v_y \end{pmatrix}= v_x\,\hat{\mathbf i} + v_y\,\hat{\mathbf j}$In 3D: $ \vec v = \begin{pmatrix} ...
Vektorzerlegung bedeutet, einen Vektor in „einfache“ Richtungsanteile zu zerlegen – typischerweise entlang von Achsen (x, y, z) oder entlang irgendeiner gewünschten Richtung. Anschaulich: Stell dir eine Pfeilspitze vor, deren „Schatten“ auf ausgewählten Richtungen wir getrennt betrachten.---1) Zerlegung entlang kartesischer AchsenIn 2D:$\vec v =\begin{pmatrix} v_x \\ v_y \end{pmatrix}= v_x\,\hat{\mathbf i} + v_y\,\hat{\mathbf j}$In 3D: $ \vec v = \begin{pmatrix} ...Konstante Vektorgeschwindigkeit
Kinematik: Beschreibung von Bewegungen > Superpositionsprinzip > Konstante Vektorgeschwindigkeit
 Liegt eine konstante Vektorgeschwindigkeit $\vec{v} = const$ vor, so bleiben Richtung und Geschwindigkeit konstant. Das bedeutet, dass hier eine lineare Funktion gegeben ist, bei welcher die Steigung in jedem Punkt gleich ist.Superpositionsprinzip: Konstante GeschwindigkeitWir wollen für diese Bewegung das Superpositionsprinzip anwenden. Es handelt es sich um eine konstante Geschwindigkeit, d.h. es tritt keine Beschleunigung auf.Beim Auftreten von Beschleunigung ändert sich die Geschwindigkeit ...
Liegt eine konstante Vektorgeschwindigkeit $\vec{v} = const$ vor, so bleiben Richtung und Geschwindigkeit konstant. Das bedeutet, dass hier eine lineare Funktion gegeben ist, bei welcher die Steigung in jedem Punkt gleich ist.Superpositionsprinzip: Konstante GeschwindigkeitWir wollen für diese Bewegung das Superpositionsprinzip anwenden. Es handelt es sich um eine konstante Geschwindigkeit, d.h. es tritt keine Beschleunigung auf.Beim Auftreten von Beschleunigung ändert sich die Geschwindigkeit ...einmalig 39,00 Euro / kein Abo
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Analysis und Gewöhnliche Differentialgleichungen
-
Binormalenvektor im Raum
Kurveneigenschaften im mehrdimensionalen Raum > Binormalenvektor im Raum
 Der Binormalenvektor $\vec{b}(t)$ ergibt sich aus dem Kreuzprodukt von Tangenteneinheitsvektor $\vec{t}_e (t)$ und dem Hauptnormalenvektor $\vec{n}(t)$,$\vec{b}(t) = \frac{\dot{\vec{r}}(t) \; \text{X} \; \ddot{\vec{r}}(t)}{|\dot{\vec{r}}(t) \; \text{X} \; \ddot{\vec{r}}(t)|} = \vec{t}_e (t) \; \text{X} \; \vec{n}(t)$.mit $\vec{r}(t)$ als Raumkurve.Das Vektorprodukt $\vec{b}(t)$ zweier Vektoren $\vec{t}_e (t), \; \vec{n}(t) \in \mathbb{R}^3$ hat die Eigenschaft, dass $\vec{b}(t)$ ...
Der Binormalenvektor $\vec{b}(t)$ ergibt sich aus dem Kreuzprodukt von Tangenteneinheitsvektor $\vec{t}_e (t)$ und dem Hauptnormalenvektor $\vec{n}(t)$,$\vec{b}(t) = \frac{\dot{\vec{r}}(t) \; \text{X} \; \ddot{\vec{r}}(t)}{|\dot{\vec{r}}(t) \; \text{X} \; \ddot{\vec{r}}(t)|} = \vec{t}_e (t) \; \text{X} \; \vec{n}(t)$.mit $\vec{r}(t)$ als Raumkurve.Das Vektorprodukt $\vec{b}(t)$ zweier Vektoren $\vec{t}_e (t), \; \vec{n}(t) \in \mathbb{R}^3$ hat die Eigenschaft, dass $\vec{b}(t)$ ... -
Richtungsableitung
Funktionen mehrerer Veränderlicher > Richtungsableitung
 ... Stelle $P$ in Richtung eines vorgegebenen Vektors für die gegebene Funktion ändert.Voraussetzungen für die RichtungsableitungUm die Richtungsableitung an einer gegebenen Stelle bestimmen zu können, benötigen wir:Eine Funktion $f(x_1, ..., x_n)$,einen Punkt (Stelle) $P(x_1, ..., x_n)$ undeinen Vektor $\vec{r}$, welcher die Richtung angibt. Sind die Voraussetzungen erfüllt, so kann die Richtungsableitung wie folgt berechnet werden:Die Richtungsableitung $D_r ...
... Stelle $P$ in Richtung eines vorgegebenen Vektors für die gegebene Funktion ändert.Voraussetzungen für die RichtungsableitungUm die Richtungsableitung an einer gegebenen Stelle bestimmen zu können, benötigen wir:Eine Funktion $f(x_1, ..., x_n)$,einen Punkt (Stelle) $P(x_1, ..., x_n)$ undeinen Vektor $\vec{r}$, welcher die Richtung angibt. Sind die Voraussetzungen erfüllt, so kann die Richtungsableitung wie folgt berechnet werden:Die Richtungsableitung $D_r ... -
Tangentenvektor
Kurveneigenschaften im ebenen Raum > Tangentenvektor
 ... gezeigt, wie generell ein Tangentenvektor bestimmt wird. Es folgt dann eine Tabelle für die unterschiedlichen Darstellungsarten von Tangentenvektoren (explizite, implizite, Parameter, Polarkoordinaten) und anschließend wird die ganze Problematik anhand von ausführlichen Beispielen veranschaulicht.EinführungZu jeder Parameterdarstellung $\vec{r}(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix}$ einer Kurve $ K $ in der Ebene definiert man den Tangentenvektor [oder ...
... gezeigt, wie generell ein Tangentenvektor bestimmt wird. Es folgt dann eine Tabelle für die unterschiedlichen Darstellungsarten von Tangentenvektoren (explizite, implizite, Parameter, Polarkoordinaten) und anschließend wird die ganze Problematik anhand von ausführlichen Beispielen veranschaulicht.EinführungZu jeder Parameterdarstellung $\vec{r}(t) = \begin{pmatrix} x(t) \\ y(t) \end{pmatrix}$ einer Kurve $ K $ in der Ebene definiert man den Tangentenvektor [oder ... -
Begleitendes Dreibein und Schmiegebene
Kurveneigenschaften im mehrdimensionalen Raum > Begleitendes Dreibein und Schmiegebene
 Der Tangenteneinheitsvektor $\vec{t}_e (t)$, der Hauptnormalenvektor $\vec{n}(t)$ und der Binormalenvektor $\vec{b}(t)$ bilden zusammen$\ (\vec{t}_e (t),\vec{n}(t),\vec{b}(t))$,die Orthonormalbasis des $\mathbb{R}^3 $. Man nennt dieses Vektorentripel das begleitende Dreibein der Kurve an der vorgegebenen Parameterstelle $\ t$. Die drei Ebenen des begleitenden DreibeinsDurch das begleitende Dreibein werden für die Kurve $\vec{r}(t)$ im Kurvenpunkt $\vec{x}_0 ...
Der Tangenteneinheitsvektor $\vec{t}_e (t)$, der Hauptnormalenvektor $\vec{n}(t)$ und der Binormalenvektor $\vec{b}(t)$ bilden zusammen$\ (\vec{t}_e (t),\vec{n}(t),\vec{b}(t))$,die Orthonormalbasis des $\mathbb{R}^3 $. Man nennt dieses Vektorentripel das begleitende Dreibein der Kurve an der vorgegebenen Parameterstelle $\ t$. Die drei Ebenen des begleitenden DreibeinsDurch das begleitende Dreibein werden für die Kurve $\vec{r}(t)$ im Kurvenpunkt $\vec{x}_0 ... -
Hauptnormalenvektor
Kurveneigenschaften im ebenen Raum > Hauptnormalenvektor
 Der Hauptnormalenvektor ist in einem bestimmten Punkt auf einer Kurve der Vektor, der senkrecht auf dem Tangentenvektor dieses Punktes liegt. Die Gerade, welche in Richtung des Normalenvektors in diesem Punkt verläuft, nennt man Normale. Die Normale ist wiederum senkrecht zur Tangente und somit auch senkrecht zur Kurve. EinführungIst der Tangentenvektor $\vec{t}(t) \not= \vec{0} $ in einem Kurvenpunkt $ (\dot{x}(t),\dot{y}(t)) $, so entsteht der Normalenvektor $\vec{n}(t)$ ...
Der Hauptnormalenvektor ist in einem bestimmten Punkt auf einer Kurve der Vektor, der senkrecht auf dem Tangentenvektor dieses Punktes liegt. Die Gerade, welche in Richtung des Normalenvektors in diesem Punkt verläuft, nennt man Normale. Die Normale ist wiederum senkrecht zur Tangente und somit auch senkrecht zur Kurve. EinführungIst der Tangentenvektor $\vec{t}(t) \not= \vec{0} $ in einem Kurvenpunkt $ (\dot{x}(t),\dot{y}(t)) $, so entsteht der Normalenvektor $\vec{n}(t)$ ... -
Richtungsfeld und Isoklinen
Gewöhnliche Differentialgleichungen > Richtungsfeld und Isoklinen
 ... aus Punkten $ (x,y) $ denen in der Ebene ein Vektor mit der Steigung $ F(x,y) $ zugeordnet wird. Jeder dieser Vektoren gibt an, welche Richtung der Graphen der Differentialgleichung hätte, sofern dieser durch den jeweiligen Punkt $ (x,y) $ verliefe.Zusammenfassend lässt sich sagen, dass sich ein Richtungsfeld sich aus all den Punkten (inkl. Vektoren) erzeugen lässt, die durch $ f(x,y) $ definiert sind. Zur Veranschaulichung siehe folgende Grafik:RichtungsfeldIsoklinenIsoklinen ...
... aus Punkten $ (x,y) $ denen in der Ebene ein Vektor mit der Steigung $ F(x,y) $ zugeordnet wird. Jeder dieser Vektoren gibt an, welche Richtung der Graphen der Differentialgleichung hätte, sofern dieser durch den jeweiligen Punkt $ (x,y) $ verliefe.Zusammenfassend lässt sich sagen, dass sich ein Richtungsfeld sich aus all den Punkten (inkl. Vektoren) erzeugen lässt, die durch $ f(x,y) $ definiert sind. Zur Veranschaulichung siehe folgende Grafik:RichtungsfeldIsoklinenIsoklinen ... -
Tangentenvektor im Raum
Kurveneigenschaften im mehrdimensionalen Raum > Tangentenvektor im Raum
 ... $ im Raum definiert man den Tangentenvektor [oder Tangentialvektor]:$\vec{t}(t) := \lim\limits_{h \to 0} \frac{1}{h} (\vec{r}(t + h) - \vec{r}(t)) = (\dot{x}(t), \ \dot{y}(t), \ \dot{z}(t))$wobei der Punkt $\dot{}$ über dem Vektor für die 1. Ableitung nach $t$ steht. Es gilt:$\dot{\vec{x}}(t) = \frac{d}{dt}x(t)$, $\dot{\vec{y}}(t) = \frac{d}{dt}y(t)$$\dot{\vec{z}}(t) = \frac{d}{dt}z(t)$.Das bedeutet also, dass man den Vektor $\vec{r}(t)$ differenziert, indem ...
... $ im Raum definiert man den Tangentenvektor [oder Tangentialvektor]:$\vec{t}(t) := \lim\limits_{h \to 0} \frac{1}{h} (\vec{r}(t + h) - \vec{r}(t)) = (\dot{x}(t), \ \dot{y}(t), \ \dot{z}(t))$wobei der Punkt $\dot{}$ über dem Vektor für die 1. Ableitung nach $t$ steht. Es gilt:$\dot{\vec{x}}(t) = \frac{d}{dt}x(t)$, $\dot{\vec{y}}(t) = \frac{d}{dt}y(t)$$\dot{\vec{z}}(t) = \frac{d}{dt}z(t)$.Das bedeutet also, dass man den Vektor $\vec{r}(t)$ differenziert, indem ... -
Parameterdarstellung
Darstellungsarten ebener Kurven > Parameterdarstellung
 ... dazu sieht wie folgt aus:ParameterdarstellungVektordarstellungUm im Weiteren die Kurveneigenschaften zu bestimmen, ist es sinnvoll die Kurve in Vektordarstellung anzugeben:$\vec{r} = (x(t), y(t)) \; \; t \in [a, b]$Der Punkt $P(x(t), y(t))$ der Kurve $K$ liegt dann in der Spitze des Vektors $\vec{x}$, welcher vom Nullpunkt ausgeht.VektordarstellungIn der obigen Grafik wird der Punkt $t_5(1,5, 2,25)$ durch den Vektor $\vec{x} = (x(t), y(t)) = (x(1,5), y(1,5)) = (1,5, \ 2,25)$ dargestellt. ...
... dazu sieht wie folgt aus:ParameterdarstellungVektordarstellungUm im Weiteren die Kurveneigenschaften zu bestimmen, ist es sinnvoll die Kurve in Vektordarstellung anzugeben:$\vec{r} = (x(t), y(t)) \; \; t \in [a, b]$Der Punkt $P(x(t), y(t))$ der Kurve $K$ liegt dann in der Spitze des Vektors $\vec{x}$, welcher vom Nullpunkt ausgeht.VektordarstellungIn der obigen Grafik wird der Punkt $t_5(1,5, 2,25)$ durch den Vektor $\vec{x} = (x(t), y(t)) = (x(1,5), y(1,5)) = (1,5, \ 2,25)$ dargestellt. ...
einmalig
39,00 Euro /
kein Abo
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Baustatik 1
-
Arbeit
Formänderungsarbeit > Arbeit
 ... definiert als das Skalarprodukt aus Kraftvektor und Wegvektor: $W = \vec{F} \cdot \vec{s} = |\vec{F}| \cdot |\vec{s}| \cos \sphericalangle (\vec{F}, \vec{s})$mit$F$ Kraftvektor$s$ Wegvektor Das Skalarprodukt berücksichtigt, dass nur der Kraftanteil mit dem ihm gleich gerichteten Weg multipliziert wird:Gegeben sei der Kraftvektor $\vec{F} = (F_x, F_y)$ und der Wegvektor $\vec{s} = (s_x, s_y)$. Bilden wir das Skalarprodukt so erhalten wir:$W = F_x \cdot s_x + F_y \cdot ...
... definiert als das Skalarprodukt aus Kraftvektor und Wegvektor: $W = \vec{F} \cdot \vec{s} = |\vec{F}| \cdot |\vec{s}| \cos \sphericalangle (\vec{F}, \vec{s})$mit$F$ Kraftvektor$s$ Wegvektor Das Skalarprodukt berücksichtigt, dass nur der Kraftanteil mit dem ihm gleich gerichteten Weg multipliziert wird:Gegeben sei der Kraftvektor $\vec{F} = (F_x, F_y)$ und der Wegvektor $\vec{s} = (s_x, s_y)$. Bilden wir das Skalarprodukt so erhalten wir:$W = F_x \cdot s_x + F_y \cdot ... -
Momente
Kurs Baustatik > Grundlagen der Statik > Momente
 Das Moment $M$ ist wie die Kraft $F$ ein Vektor, was symbolisch durch $\vec{M}$ ausgedrückt wird.In der nächsten Abbildung siehst du die Schiffschleuse in Falkirk (Schottland): Schleuse in FalkirkDiese Schleuse nutzt Drehmomente um Binnenschiffe von einer Ebene auf eine andere Ebene zu senken/heben. Hierzulande werden Schleusen hingegen geflutet oder Wasser abgelassen.Der Vektor des Drehmoments $\vec{M}$ ergibt sich aus dem Kreuzprodukt aus Ortsvektor und Kraftvektor:$\vec{M} = \vec{r} \times ...
Das Moment $M$ ist wie die Kraft $F$ ein Vektor, was symbolisch durch $\vec{M}$ ausgedrückt wird.In der nächsten Abbildung siehst du die Schiffschleuse in Falkirk (Schottland): Schleuse in FalkirkDiese Schleuse nutzt Drehmomente um Binnenschiffe von einer Ebene auf eine andere Ebene zu senken/heben. Hierzulande werden Schleusen hingegen geflutet oder Wasser abgelassen.Der Vektor des Drehmoments $\vec{M}$ ergibt sich aus dem Kreuzprodukt aus Ortsvektor und Kraftvektor:$\vec{M} = \vec{r} \times ...
einmalig
39,00 Euro /
kein Abo
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Technische Mechanik 3: Dynamik
-
Ort-Zeit-Diagramm
Kinematik eines Massenpunktes > Geradlinige Bewegung eines Massenpunktes > Kinematische Grundaufgaben > Kinematische Diagramme > Ort-Zeit-Diagramm
 ... in einem Punkt, welche mittels Tangentenvektor (rot) gekennzeichnet ist. Die Geschwindigkeit kann anhand der Steigung in diesem Punkt bestimmt werden durch:$v = \frac{dx}{dt}$.Je größer die Steigung, desto höher die Geschwindigkeit. Im ersten Punkt bei $t = 1$ ist die Steigung kleiner als im Punkt bei $t = 9$. Das bedeutet also, dass die Geschwindigkeit im Punkt $P(t = 9)$ größer ist. Bei einer negativen Steigung existiert eine negative Geschwindigkeit. Diese ...
... in einem Punkt, welche mittels Tangentenvektor (rot) gekennzeichnet ist. Die Geschwindigkeit kann anhand der Steigung in diesem Punkt bestimmt werden durch:$v = \frac{dx}{dt}$.Je größer die Steigung, desto höher die Geschwindigkeit. Im ersten Punkt bei $t = 1$ ist die Steigung kleiner als im Punkt bei $t = 9$. Das bedeutet also, dass die Geschwindigkeit im Punkt $P(t = 9)$ größer ist. Bei einer negativen Steigung existiert eine negative Geschwindigkeit. Diese ... -
Beispiele: Geschwindigkeitsvektor aus Bahnkurve
Kinematik eines Massenpunktes > Allgemeine Bewegung eines Massenpunktes > Geschwindigkeit eines Massenpunktes > Geschwindigkeitsvektor > Beispiele: Geschwindigkeitsvektor aus Bahnkurve
 ... zum Thema Geschwindigkeitsvektor vor.Beispiel zum GeschwindigkeitsvektorGegeben sei die folgende Bahnkurve: $r(t) = (2t, 4t, 0t)$. Wie sieht der Geschwindigkeitsvektor zur Zeit $t = 1$ aus? Der Punkt um den es sich hier handelt ist: $P(2,4,0)$ (Einsetzen von $t = 1$).$ \rightarrow $ Die Geschwindigkeit bestimmt sich durch die Ableitung der Bahnkurve nach der Zeit $t$:$\vec{v} = \dot{r} = (2,4,0)$. Man weiß nun also, in welche Richtung der Geschwindigkeitsvektor ...
... zum Thema Geschwindigkeitsvektor vor.Beispiel zum GeschwindigkeitsvektorGegeben sei die folgende Bahnkurve: $r(t) = (2t, 4t, 0t)$. Wie sieht der Geschwindigkeitsvektor zur Zeit $t = 1$ aus? Der Punkt um den es sich hier handelt ist: $P(2,4,0)$ (Einsetzen von $t = 1$).$ \rightarrow $ Die Geschwindigkeit bestimmt sich durch die Ableitung der Bahnkurve nach der Zeit $t$:$\vec{v} = \dot{r} = (2,4,0)$. Man weiß nun also, in welche Richtung der Geschwindigkeitsvektor ...
einmalig
39,00 Euro /
kein Abo
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Technische Mechanik 1: Statik
-
Resultierende grafisch bestimmen
Einzelkräfte mit gemeinsamen Angriffspunkt > Resultierende grafisch bestimmen
 ... Konstruktion entspricht einer grafischen Vektoraddition. Hierbei werden die auf den Körper wirkenden Kräfte in einer beliebigen Reihenfolge aneinandergereiht. Die Resultierende ergibt sich dann aus dem Anfangspunkt des Anfangsvektors und dem Endpunkt des Endvektors. Grafische Vektoraddition Die grafische Vektoraddition von Kräften wird auch Kräftepolygon genannt. Das Kräftepolygon in einer Ebene ist einfach die zeichnerische Verbindung aller Kräfte ...
... Konstruktion entspricht einer grafischen Vektoraddition. Hierbei werden die auf den Körper wirkenden Kräfte in einer beliebigen Reihenfolge aneinandergereiht. Die Resultierende ergibt sich dann aus dem Anfangspunkt des Anfangsvektors und dem Endpunkt des Endvektors. Grafische Vektoraddition Die grafische Vektoraddition von Kräften wird auch Kräftepolygon genannt. Das Kräftepolygon in einer Ebene ist einfach die zeichnerische Verbindung aller Kräfte ...
einmalig
39,00 Euro /
kein Abo
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Elektrotechnik
-
Physikalische Größen
Gleichstrom > Elektrische Größen > Physikalische Größen
 ... Wertes als potentielle Energie) Angabe von VektorenFormal werden Vektoren durch einen Pfeil über dem Formelzeichen angegeben. Ein Vektor gehört zu den physikalischen Größen, die neben dem Betrag / Zahlenwert auch eine Richtung angeben. Diese werden Ihnen besonders bei den Themen elektrische und magnetische Feldstärke erneut begegnen. BeispielVektor für eine Kraft: $\vec{F} $ Angabe von zeitveränderlichen GrößenTreten in einer Gleichung ...
... Wertes als potentielle Energie) Angabe von VektorenFormal werden Vektoren durch einen Pfeil über dem Formelzeichen angegeben. Ein Vektor gehört zu den physikalischen Größen, die neben dem Betrag / Zahlenwert auch eine Richtung angeben. Diese werden Ihnen besonders bei den Themen elektrische und magnetische Feldstärke erneut begegnen. BeispielVektor für eine Kraft: $\vec{F} $ Angabe von zeitveränderlichen GrößenTreten in einer Gleichung ...
einmalig
39,00 Euro /
kein Abo
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Technische Mechanik 2: Elastostatik
-
Allgemeine Annahmen
Mehrachsige Spannungszustände > Allgemeine Annahmen
 ... der Spannungen herangezogen:Lokaler Spannungsvektor In der obigen Grafik greifen die Kräfte beliebig am Körper an. Die Kräfte greifen nun also nicht mehr nur in Richtung der Längsachse des Körpers (wie bei Zugstäben/Druckstäben) an. Bei einem Zug-/Druckstab war es so, dass nur Kräfte in einer Achsenrichtung aufgetreten sind:Beanspruchung eines Zugstabs Bei einem Schnitt und dem Abtragen der Schnittkräfte $N$ (senkrecht) auf der Schnittfläche, ...
... der Spannungen herangezogen:Lokaler Spannungsvektor In der obigen Grafik greifen die Kräfte beliebig am Körper an. Die Kräfte greifen nun also nicht mehr nur in Richtung der Längsachse des Körpers (wie bei Zugstäben/Druckstäben) an. Bei einem Zug-/Druckstab war es so, dass nur Kräfte in einer Achsenrichtung aufgetreten sind:Beanspruchung eines Zugstabs Bei einem Schnitt und dem Abtragen der Schnittkräfte $N$ (senkrecht) auf der Schnittfläche, ...
einmalig
39,00 Euro /
kein Abo
umsatzsteuerbefreit gem. § 4 Nr. 21 a bb) UStG
Webinare
-
Crashkurs: Statik – Mit Erfolg deine Klausur bestehen - Tag 2
...n>rechnung Kräfte und Kräftesystem Gleichgewichtsbedingungen Stabkraftberechnung und Haftung und Reibung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Deine Vorteile: Kompakte Zusammenfassung der wichtigsten Inhalte Anschauliche Erklärungen und praxisnahe Beispiele Gelegenheit, Deine Fragen direkt an den Dozenten zu stellen Weiter Webinare Melde dich doch auf für unsere andere... -
Crashkurs: Statik – Mit Erfolg deine Klausur bestehen
...n>rechnung Kräfte und Kräftesystem Gleichgewichtsbedingungen Stabkraftberechnung und Haftung und Reibung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Deine Vorteile: Kompakte Zusammenfassung der wichtigsten Inhalte Anschauliche Erklärungen und praxisnahe Beispiele Gelegenheit, Deine Fragen direkt an den Dozenten zu stellen Weiter Webinare Melde dich doch auf für unsere andere... -
Crashkurs - Mathematik 1
...:#FFFF66; color:#FF0000;">Vektorrechnung Matrizen und deren Eigenschaften Vektorräume Reelle und komplexe Zahlen Elementare Funktionstypen, z. B. rationale und irrationale Funktionen Differential- und Integralrechnung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Anhand von Beispielaufgaben wiederholst du... -
Crashkurs: Statik – Mit Erfolg deine Klausur bestehen
...n>rechnung Kräfte und Kräftesystem Gleichgewichtsbedingungen Stabkraftberechnung und Haftung und Reibung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Deine Vorteile: Kompakte Zusammenfassung der wichtigsten Inhalte Anschauliche Erklärungen und praxisnahe Beispiele Gelegenheit, Deine Fragen direkt an den Dozenten zu stellen Weiter Webinare Melde dich doch auf für unsere andere... -
Crashkurs - Mathematik 1
...:#FFFF66; color:#FF0000;">Vektorrechnung Matrizen und deren Eigenschaften Vektorräume Reelle und komplexe Zahlen Elementare Funktionstypen, z. B. rationale und irrationale Funktionen Differential- und Integralrechnung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Anhand von Beispielaufgaben wiederholst du... -
Crashkurs: Statik
...und-color:#FFFF66; color:#FF0000;">Vektorrechnung Kräfte und Kräftesystem Gleichgewichtsbedingungen Stabkraftberechnung und Haftung und Reibung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Weiter Webinare Melde dich doch auf für unsere anderen Webinare an: Crashkurs: Fluidmechanik am 27.01.24 Crashkurs: Thermodynamik am 03.02.24 Crashkurs: Maschinenelemente 2 am 05.02.24 und 07.02.24... -
Crashkurs - Mathematik 1
...:#FFFF66; color:#FF0000;">Vektorrechnung Matrizen und deren Eigenschaften Vektorräume Reelle und komplexe Zahlen Elementare Funktionstypen, z. B. rationale und irrationale Funktionen Differential- und Integralrechnung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Anhand von Beispielaufgaben wiederholst du... -
Crashkurs: Statik
...und-color:#FFFF66; color:#FF0000;">Vektorrechnung Kräfte und Kräftesystem Gleichgewichtsbedingungen Stabkraftberechnung und Haftung und Reibung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Über deinen Dozenten MSc. Kevin Suta bereitet seit Jahren Studieren auf ihre Prüfungen im Ingenieurstudium vor. Er ist Master of Science in Materialwissenschaft & Werkstofftechnik an der Unive... -
Crashkurs: Thermodynamik
...or:#FFFF66; color:#FF0000;">Vektorrechnung Kräfte und Kräftesystem Gleichgewichtsbedingungen Stabkraftberechnung Haftung und Reibung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Über deinen Dozenten MSc. Kevin Suta bereitet seit Jahren Studenten auf ihre Prüfungen im Ingenieurstudium vor. Er ist Master of Science in Materialwissenschaft & Werkstofftechnik an der Universität Si... -
Crashkurs: Statik
...und-color:#FFFF66; color:#FF0000;">Vektorrechnung Kräfte und Kräftesystem Gleichgewichtsbedingungen Stabkraftberechnung und Haftung und Reibung Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Über deinen Dozenten MSc. Kevin Suta bereitet seit Jahren Studenten auf ihre Prüfungen im Ingenieurstudium vor. Er ist Master of Science in Materialwissenschaft & Werkstofftechnik an der Unive... -
Crashkurs: Statik
...-color:#FFFF66; color:#FF0000;">Vektorrechnung, Kräfte und Kräftesystem, Gleichgewichtsbedingungen, Stabkraftberechnung und Haftung und Reibung. Zu allen Themen werden die besonders wichtigen Inhalte besprochen und du kannst Rückfragen an unseren Dozenten stellen. Über deinen Dozenten MSc. Kevin Suta bereitet seit Jahren Studenten auf ihre Prüfungen im Ingenieurstudium vor. Er ist Master of Science in Materialwissenschaft & Werkstofftechnik an... -
Klausurbesprechung Statik
...ng, Mechanische Modelle und Schnittprinzip Zentrales Kräftesystem: Resultierende, Kräftezerlegung, Gleichgewichtsbedingungen Nicht-zentrales ebenes Kräftesystem: Resultierende, Kräftezerlegung, Gleichgewicht Allgemeines räumliches Kräftesystem Balkenstrukturen: Lagerung, Berechnung der LagerreaktionenInnere Kräfte und Momente, Einzelkräfte und verteilte Lasten Fachwerke: statische Bestimmtheit, Nullstäbe, Stabkraftberechnung Haftung und Reibung: Phänomene, Berechnu... -
Crashkurs: Statik
...olor:#FF0000;">Vektorrechnung, Mechanische Modelle und Schnittprinzip Zentrales Kräftesystem: Resultierende, Kräftezerlegung, Gleichgewichtsbedingungen Nicht-zentrales ebenes Kräftesystem: Resultierende, Kräftezerlegung, Gleichgewicht Allgemeines räumliches Kräftesystem Balkenstrukturen: Lagerung, Berechnung der LagerreaktionenInnere Kräfte und Momente, Einzelkräfte und verteilte Lasten Fachwerke: statische Bestimmtheit, Nullstäbe, Stabkraftberechnung Haftung und Reibung: P... -
Gratis-Webinar Höhere Mathematik 1 - Vektorrechnung
...kt....









