Inhaltsverzeichnis
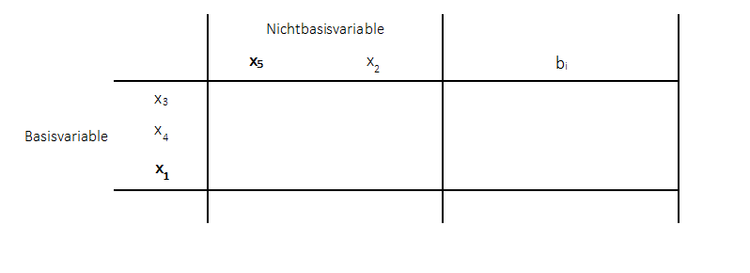
Im vorangegangenen Abschnitt wurde gezeigt, wie die Pivotspalte, die Pivotzeile und das Pivotelemet ausgewählt werden. In diesem Abschnitt sollen jetzt die Werte des neuen Tableaus bestimmt werden, nachdem die Basisvariable der Pivotzeile mit der Nichtbasisvariablen der Pivotspalte vertauscht worden ist. Das neue Tableau sieht nun zunächst wie folgt aus:
Ein Austauschschritt entspricht exakt einem Schritt beim Lösen eines linearen Gleichungssystems, bei dem man die Pivotzeile $s$ nach der Variablen $x_t$ (hier: $x_1$) auflöst und dann $x_1$ in die restlichen Gleichungen einsetzt.
Simplexschritt
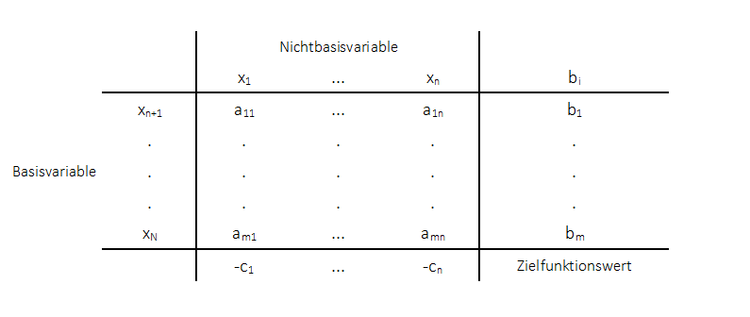
Bei einem Austauschschritt berechnet sich das neue Simplextableau folgendermaßen:
Methode
Pivotelement: $a_{st} = \frac{1}{a_{st}}$
Dort wo das Pivotelement stand wird der neue Wert bestimmt, indem der Kehrwert gebildet wird: $\frac{1}{\text{Pivotelement}}$.
Methode
Pivotzeile $s$:
$a_{sj} = \frac{a_{sj}}{a_{st}}$
$b_{s} = \frac{b_r}{a_{st}}$
Die neuen Werte in der Pivotzeile werden bestimmt, indem die alten Werte durch das Pivotelement dividiert werden. Dies gilt auch für den Wert der rechten Seite der Pivotzeile.
Methode
Pivotspalte $t$:
$a_{it} = - \frac{a_{it}}{a_{st}}$
$c_t = - \frac{c_t}{a_{st}}$
Die neuen Werte der Pivotspalte werden bestimmt, indem die alten Werte durch das Pivotelement dividiert und mit einem Minuszeichen versehen werden. Dies gilt auch für den neuen Wert der Zielfunktionszeile der Pivotspalte.
Methode
Restliche Elemente:
$a_{ij} = a_{ij} - \frac{a_{it} \cdot a_{sj}}{a_{st}}$
$c_j = c_j - \frac{c_t \cdot a_{sj}}{a_{st}}$
$b_i = b_i - \frac{b_s \cdot a_{it}}{a_{st}}$
Die restlichen Werte werden bestimmt, indem von dem alten Wert das Produkt aus zugehörigem Element der Pivospalte und Pivotzeile dividiert mit dem Pivotelemet abgezogen wird.
Diese Rechenschritte müssen durchgeführt werden, damit das neue Tableau mit verbessertem Zielfunktionswert ermittelt werden kann.
Beispiel: Simplexschritt
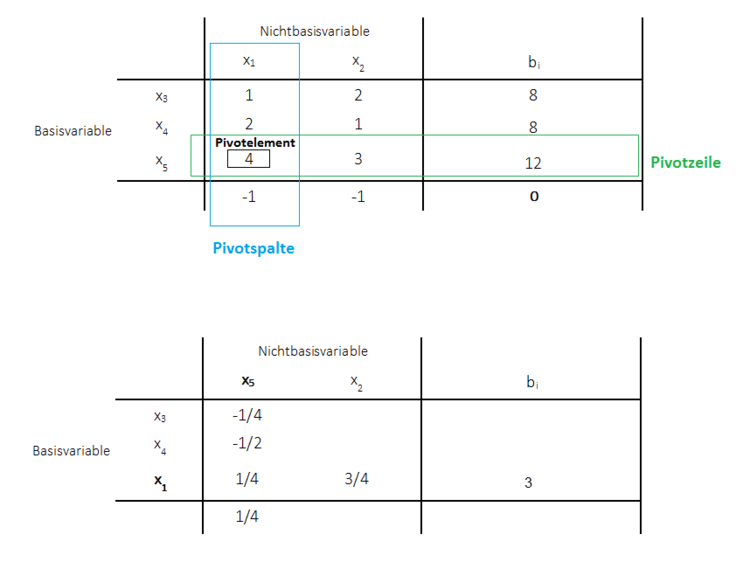
Das ganze Vorgehen wird im Nachfolgenden anhand des Beispiels aus dem vorherigen Abschnitt aufgezeigt.
- Dort wo im alten Tableau das Pivotelement ($4$) stand, wird nun das neue Element ermittelt durch: 1/Pivotelement, d.h. also $\frac{1}{4}$.
- Die neuen Elemente der Pivotzeile werden bestimmt indem die alten Elemente durch das Pivotelement dividiert werden: Neue Elemente = Alte Elemente/Pivotelement, z.B. $a_{32} = \frac{3}{4}$.
- Die neuen Elemente der Pivotspalte werden bestimmt, indem die alten Elemente durch das Pivotelement dividiert werden und mit $-1$ multipliziert werden: Neue Elemente = Alte Elemente/Pivotelement, z.B. $a_{11} = -\frac{1}{4}$
Es sind nun alle alten Element der Pivotzeile und Pivotspalte ausgetauscht worden. Es fehlen nun noch die restlichen Werte, diese werden wie folgt bestimmt:
Die Vorgehensweise ist wie folgt:
$\text{Neues Element}$
$= \text{Altes Element} - \frac{\text{entsprechendes Element der Pivotzeile} \cdot \text{entsprechendes Element der Pivotspalte}}{\text{Pivotelement}}$.
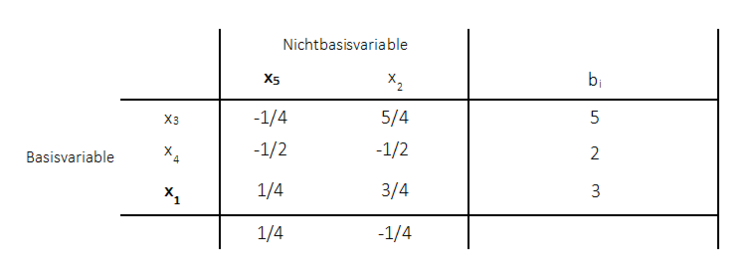
Für diese restlichen Werte wird die Berechnung nochmals separat aufgeführt:
$\frac{5}{4} = 2 - \frac{1 \cdot 3 }{4}$
$-\frac{1}{2} = 1 - \frac{2 \cdot 3}{4}$
$-\frac{1}{4} = -1 - \frac{-1 \cdot 3}{4}$
$5 = 8 - \frac{1 \cdot 12}{4}$
$2 = 8 - \frac{2 \cdot 12}{4}$
Basislösung
Aufgrund der Durchführung eines Simplexschrittes resultiert eine neue Basislösung. Dabei besitzen die Nichtbasisvariablen immer den Wert Null $x_5 = 0$ und $x_2 = 0$ und die Basisvariablen immer den Wert der rechten Seite: $x_3 = 5$, $x_4 = 2$ und $x_1 = 3$.
Der Zielfunktionswert ist bei dieser zweiten Basislösung:
$f(0,0) = 1 \cdot 3 + 1 \cdot 0 = 3$
Der Zielfunktionswert hat sich demnach verbessert. Bei der ersten Basislösung besaß dieser noch den Wert null und ist nun nach einem Simplexschritt auf den Wert 3 angestiegen. Es handelt sich hierbei wieder um eine zulässige Basislösung, allerdings noch nicht um die optimale Basislösung, da noch ein negativer Wert in der Zielfunktionszeile steht (-1/4).
Weitere interessante Inhalte zum Thema
-
Obere Schranken: Vielzahl an beschränkten Variablen
Vielleicht ist für Sie auch das Thema Obere Schranken: Vielzahl an beschränkten Variablen (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.
-
Primaler Simplexalgorithmus
Vielleicht ist für Sie auch das Thema Primaler Simplexalgorithmus (Grundlagen des Operations Research 1) aus unserem Online-Kurs Operations Research 2 interessant.