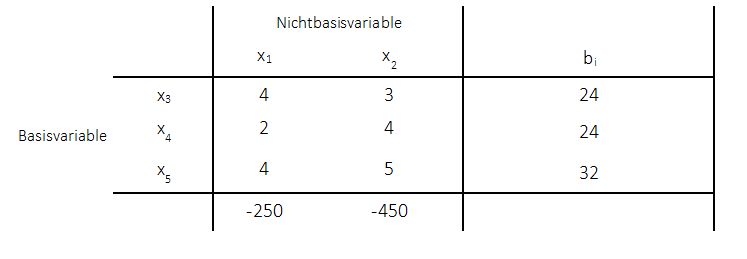Inhaltsverzeichnis
Nachdem das Tableau für das lineare Optimierungsproblem im vorherigen Abschnitt aufgestellt worden ist, soll nun die erste Iteration für das primale Simplexverfahren durchgeführt werden. Für jede Iteration müssen die folgenden Schritte durchgeführt werden:
- Wahl der PivotSpalte t: Enthält die untere Zeile, in welcher die Werte aus der Zielfunktion eingetragen werden, nur nicht-negative Werte, so ist die optimale Lösung gefunden. Ansonsten wird diejenige Spalte mit dem kleinsten negativen Wert ausgewählt. Sind mehrere Spalten mit kleinstem negativen Wert gegeben, so kann unter diesen eine beliebige Spalte ausgewählt werden.
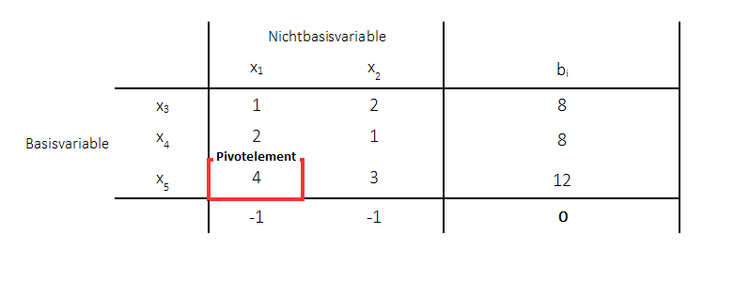
- Wahl der Pivotzeile s: Sind in der Pivotspalte aus 1. alle $a_{it} \le 0$, so exsitiert für das Problem keine optimale Lösung. Das Verfahren muss abgebrochen werden. Ansonsten wird die rechte Seite für alle Elemente $a_{it} \ge 0$ der Pivotspalte betrachtet und diejenige Pivotzeile ausgewählt, für die gilt $min\frac{bi}{a_{it}}$. Dort wo sich die Pivotspalte und die Pivotzeile schneiden, liegt das Pivotelement $a_{st}$.
- Nachdem die Pivotspalte $t$ und die Pivotzeile $s$ sowie das Pivotelement $a_{st}$ bestimmt worden sind, wird nun in einem nächsten Schritt die Basisvariable der Pivotzeile mit der Nichtbasisvarbiablen der Pivotspalte getauscht und ein neues Tableau aufgestellt.
Merke
Die Optimallösung des Maximierungsproblems liegt nach dem primalen Simplexverfahren dann vor, wenn alle Werte der Zielfunktionszeile positiv sind.
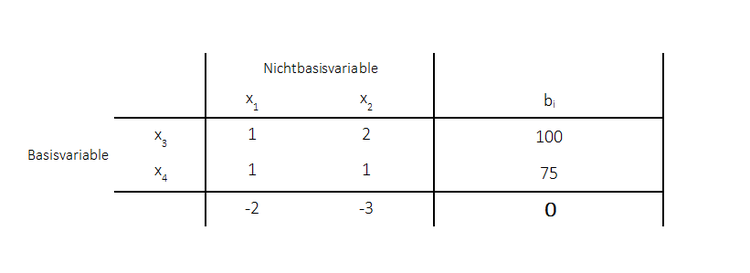
Zum besseren Verständnis der ersten drei Schritte, wird nun das Beispiel aus dem vorherigen Abschnitt herangezogen und ausführlich gezeigt, wie diese Schritte durchgeführt werden:
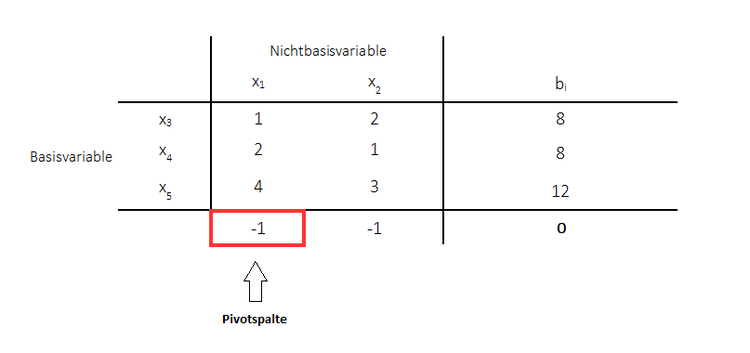
1. Schritt: Wahl der Pivotspalte
Es wird diejenige Spalte als Pivotspalte ausgewählt, für welche der Zielfunktionswert den kleinsten negativen Wert annimmt. In dem obigen Beispiel sind beide Werte gleich (-1). Das bedeutet, es kann eine beliebige Spalte als Pivotspalte gewählt werden. In diesem Fall ist nun die erste Spalte gewählt worden.
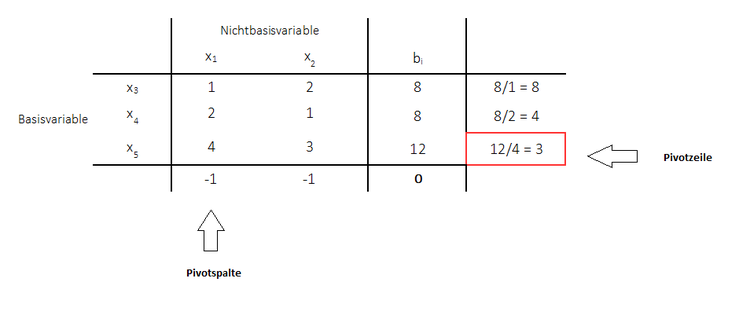
2. Schritt: Wahl der Pivotzeile
Als nächstes werden dann alle Werte innerhalb der Pivotspalte betrachtet (hier: 4, 2, 1). Es werden dann diejenigen Werte größer Null ausgewählt (die kleiner gleich null bleiben unberücksichtigt) und mit den Werten der rechten Seiten verrechnet (Division der rechten Seiten durch die Werte). Dort wird der kleinste Wert ausgewählt und die Pivotzeile festgelegt. Das Pivotelement liegt dann dort, wo sich Pivotspalte und Pivotzeile schneiden:
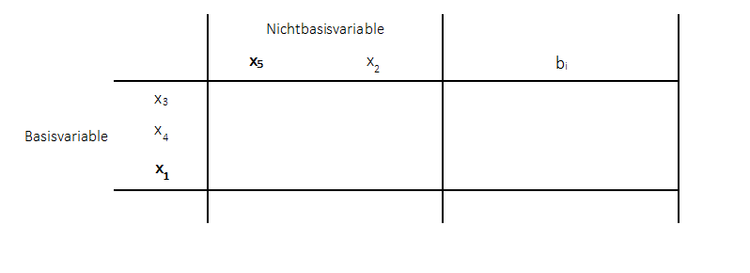
3. Schritt: Aufstellen eines neuen Tableaus, wobei Basisvariable mit Nichtbasisvariable vertauscht werden:
Dies sind die ersten drei Schritte, die durchgeführt werden müssen. Es kann nun das neue Tableau aufgestellt werden, welches zunächst noch leer ist. Die Basisvariable der Pivotzeile $x_5$ und die Nichtbasisvariable der Pivotspalte $x_1$ sind vertauscht worden. Für die Bestimmung der neuen Werte des Tableaus müssen nun einige Rechenschritte durchgeführt werden, die im folgenden Abschnitt erläutert werden.
Weitere interessante Inhalte zum Thema
-
Obere Schranken
Vielleicht ist für Sie auch das Thema Obere Schranken (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.
-
Beispiel: Maximierungsproblem / Primales Simplexverfahren
Vielleicht ist für Sie auch das Thema Beispiel: Maximierungsproblem / Primales Simplexverfahren (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.