Inhaltsverzeichnis
In diesem Abschnitt wird das Matrixminimumverfahren angewandt.
Matrixminimumverfahren - Definition
Es handelt sich hierbei um ein Eröffnungsverfahren für Transportprobleme zur Erzielung einer zulässigen Ausgangslösung.
Die Vorgehensweise des Matrixminimumverfahrens ist eine Kombination aus dem Spalten- und Zeilenfolgeverfahren.
Methode
Matrixminimumverfahren
Zu Beginn des Verfahrens sind alle Zeilen und Spalten unmarkiert.
1. Es wird das kleinste Element der Matrix ausgewählt. Bei mehreren gleich kleinen Elemente, wird ein bliebiges Element gewählt.
2. Es wird dann $x_{ij} = min \{a_i, b_j \}$ gesetzt. Danach werden die Angebots- und Nachfragemengen angepasst durch $a_i := a_i - x_{ij} $ und $b_j := b_j - x_{ij}$.
Ist danach $a_i = 0$, wird die Zeile $i$ markiert und die Elemente dieser Zeile für die weiteren Betrachtungen nicht weiter berücksichtigt. Ist danach $b_j = 0$ wird die Spalte $j$ markiert und die Elemente der Spalte für die weiteren Betrachtungen nicht weiter berücksichtigt.
Ist danach sowohl Angebotsmenge als auch Nachfragemenge Null, also $a_i = b_j = 0$, so wird das nächsthöhere Element der Zeile ausgewählt und 0 eingesetzt. Dies geschieht, damit am Ende $m + n - 1$-Basisvariablen resultieren.
Es geht dann weiter mit Schritt 1 und dem kleinsten Element der Matrix, wobei die markierten Spalten und Zeile nicht mehr berücksichtigt werden düfen.
Das Verfahren ist abgeschlossen, wenn alle Spalten und Zeilen markiert sind.
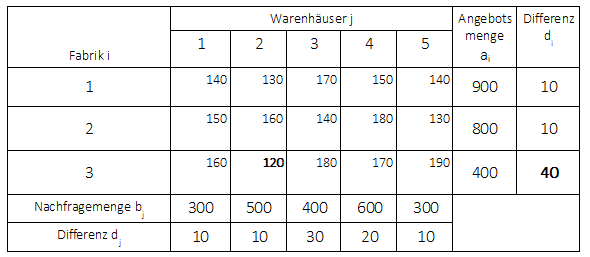
Für das Matrixminimumverfahren wird die Mengenmatrix benötigt:
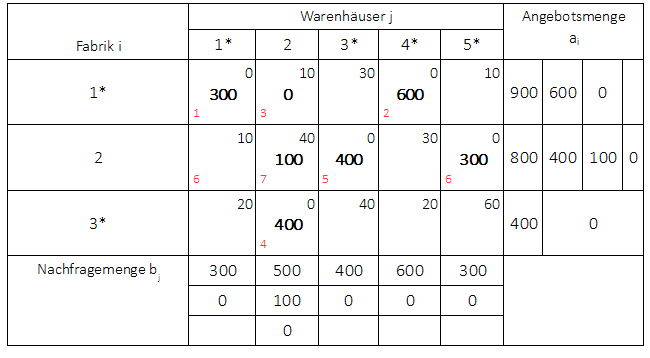
In die Mengenmatrix werden die reduzierten Kosten (sofern eine Reduktion der Kostenmatrix vorgenommen wurde, sonst die Kosten der Ausgangsmatrix) an die rechte obere Ecke geschrieben. Die Mengenbelegung nach Durchführung des Matrixminimumverfahrens ergibt sich wie folgt:
Transportkosten
Die gesamten reduzierten Transportkosten betragen:
$K_R = 300 \cdot 0 + 0 \cdot 10 + 100 \cdot 40 + 400 \cdot 0 + 400 \cdot 0 + 600 \cdot 0 + 300 \cdot 0 = 4.000$
Die tatsächlichen Transportkosten betragen:
$K = 300 \cdot 140 + 0 \cdot 130 + 100 \cdot 160 + 400 \cdot 120 + 400 \cdot 140 + 600 \cdot 150 + 300 \cdot 130 = 291.000$.
Merke
Das Spalten- und Zeilenfolgeverfahren sowie das Matrixminimumverfahren führen nicht immer zu den selben Transportkosten, ermitteln aber eine weitaus bessere Ausgangslösung als das Nord-West-Ecken-Verfahren.
Weitere interessante Inhalte zum Thema
-
Vogelsches-Approximations-Verfahren
Vielleicht ist für Sie auch das Thema Vogelsches-Approximations-Verfahren (Transport- und Zuordnungsprobleme) aus unserem Online-Kurs Operations Research 1 interessant.
-
Spaltenfolgeverfahren
Vielleicht ist für Sie auch das Thema Spaltenfolgeverfahren (Transport- und Zuordnungsprobleme) aus unserem Online-Kurs Operations Research 1 interessant.