Inhaltsverzeichnis
In diesem Kurstext behandeln wir den magnetischen Fluss, die Durchflutung und die dazugehörigen Berechnungsgrundlagen.
Magnetischer Fluss
Als magnetischen Fluss bezeichnet man die Summe aller magnetischen Feldlinien und dieser wird in der Einheit $Vs $ angegeben. Da die Feldlinien - abhängig von ihrer Lage - eine unterschiedliche Dichte aufweisen, gilt es zudem die magnetische Flussdichte [bzw. magn. Induktion] zu bestimmen. Man drückt die Flussdichte durch den Vektor $\vec{B} $ aus. Man muss einen Vektor verwenden, da die magnetischen Feldlinien eine ortsabhängige Orientierung besitzen.
Methode
Man kann die Einheit der magnetischen Flussdichte auch aus der Einheit des magnetischen Flusses $ 1 Vs $ ableiten.
Methode
Formal beschreibt man den magnetischen Fluss dann durch:
Methode
Erfasst man mit der Fläche A alle auftretenden Feldlinien, so erhält man aus der Integration den Gesamtfluss.
Sind nicht alle Feldlinien in der Fläche A enthalten, so umfasst das Ergebnis nur einen Teilfluss.
Bei der Bestimmung ist es nicht zwingend erforderlich, dass die Flächennormale $ d \vec{A} $ parallel zu den Feldlinien steht.
Sonderfall homogenes magnetisches Feld
Existieren in einem magnetischen Feld Bereiche in denen eine Homogenität vorliegt, so lässt sich für diesen Bereich der magnetische Fluss vereinfacht errechnen durch
Methode
Analogien zwischen elektrischen und magnetischen Feldern
Nachfolgend siehst du in der Tabelle die Analogien, die zwischen elektrischen und magnetischen Feldern bestehen. Einzige Ausnahme in der Beschreibung ist, dass beim elektrischen Strom wirklich eine Bewegung stattfindet.
| Feld | Strom | Dichte | Bewegung |
| Elektrisches Strömungsfeld | elektrischer Strom | Stromdichte | Ladungsträgerbewegung |
| Magnetisches Strömungsfeld | magnetischer Fluss | magnetischer Flussdichte | keine Bewegung |
Durchflutung
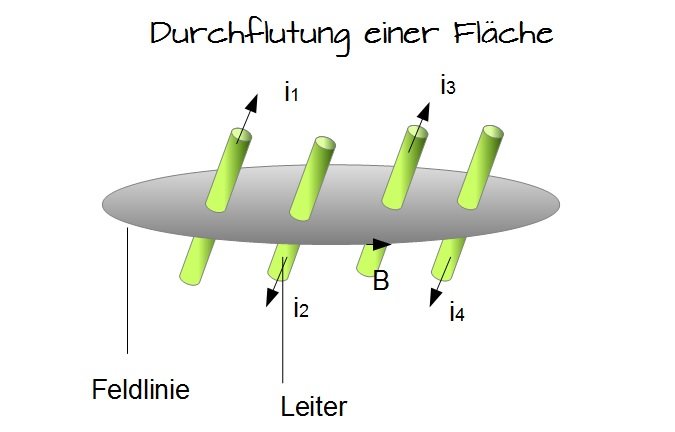
Man stelle sich eine Fläche $ A $ vor. Durch diese Fläche strömen Ladungsträger mit der Eigenschaft, dass sie zueinander eine beliebige Richtung und Intensität aufweisen. Zudem wissen wir, dass durch die Bewegung der Ladungsträger ein Magnetfeld entsteht.
Merke
Diese Durchflutung wird formal beschrieben durch
Methode
Nun verändern wir die Ausgangssituation dahin gehend, dass die besagte Fläche nicht mehr ganzflächig von Ladungsträgern durchströmt wird, sondern von einer beliebigen Anzahl von elektrischen Leitern, in denen sich Ladungsträger in unterschiedlicher Richtung und Intensität bewegen. Unter dieser Voraussetzung ändert sich die formale Beschreibung der Durchflutung, indem man die einzelnen Stromdichten der Leiter aufsummiert:
Methode
Beispiel
In der Abbildung verlaufen die Ströme von $ i_1 $ und $ i_3 $, sowie die Ströme $ i_2 $ und $ i_4 $ in die gleiche Richtung. Stellen wir nun die Gleichung für die Durchflutung auf:
$\Theta = i_1 - i_2 + i_3 - i_4 $
Möchte man, dass die Durchflutung den Wert null annimmt, muss man die Ströme derart anpassen, sodass gilt
$ i_1 - i_2 + i_3 - i_4 = 0 $ oder $\rightarrow i_1 + i_3 = i_2 + i_4 $.
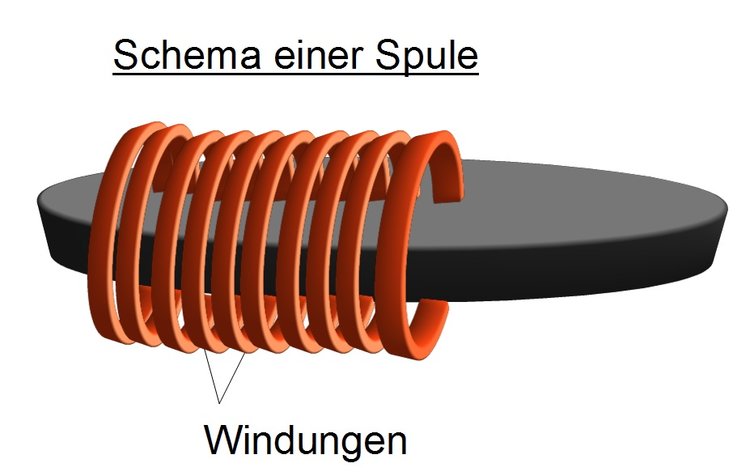
Spule
Wenn man nun nicht mehr mehrere Leiter betrachtet, sondern nur einen Leiter, der die oben abgebildete Fläche mehrfach durchläuft, so haben wir eine Spule. Dies vereinfacht unsere Rechnung erheblich, da nun lediglich ein Strom $ i $ und eine Stromdichte $ S $ vorliegt. Verändern kann sich der Wert unserer Durchflutung, wenn man davon ausgeht, dass der Strom konstant ist, demnach nur, wenn man die Anzahl der Durchläufe [Windungen] variiert:
Durchflutung für einen Strom mit mehreren Windungen:
Methode
N = Windungszahl der Spule