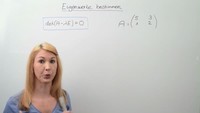Inhaltsverzeichnis
Im diesem Kurstext zeigen wir dir die Berechnung der Eigenvektoren zu verschiedenen Eigenwerten.
Der zu dem Eigenwert $\lambda$ gehörende Eigenvektor $\vec{x}$ ist die Lösung der Gleichung
$(A - \lambda E)\vec{x} = 0$, wobei $\vec{x} \neq \vec{0}$ gilt.
Anwendungsbeispiel
Beispiel
Gegeben sei die Matrix aus dem vorherigen Beispiel $A = \begin{pmatrix} 3 & 0 \\ -4 & 5 \end{pmatrix}$ mit den Eigenwerten $\lambda_1 = 5, \lambda_2 = 3$. Berechne die zugehörigen Eigenvektoren zu $\lambda_1$ und $\lambda_2$!
Berechnung des 1. Eigenvektors
Aus $\lambda_1 = 5$ folgt:
$(A - 5 E)\vec{x} = 0$
$= \begin{pmatrix} 3 & 0 \\ -4 & 5 \end{pmatrix} - 5 \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$
$= \begin{pmatrix} 3 - 5 & 0 \\ -4 & 5 - 5 \end{pmatrix}$
Ergebnis mit dem $\vec{x}$ multiplizieren und gleich Null setzen:
$= \begin{pmatrix} -2 & 0 \\ -4 & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = 0$
$= \begin{pmatrix} -2x_1 + 0x_2 \\ -4x_1 + 0x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$
D. h. es ist folgendes Gleichungssystem zu lösen:
$-2x_1 + 0x_2 = 0$ $\rightarrow x_1 =0$
$-4x_1 + 0x_2 = 0$ $\rightarrow x_1 =0$
Es gilt schonmal $x_1 = 0$. Da $\vec{x} \neq \vec{0}$, muss $x_2$ einen Wert ungleich Null annehmen. Wir setzen $x_2 = 1$. So ist z.B. der Vektor $\vec{x} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$ eine Lösung des Problems, denn:
$\begin{pmatrix} -2 & 0 \\ -4 & 0 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \; $ ergibt $ \; \begin{pmatrix} 0 \\ 0 \end{pmatrix} $
Berechnung des 2. Eigenvektors
$\lambda_2 = 3$:
$(A - 3 E)\vec{x} = 0$:
$= \begin{pmatrix} 3 & 0 \\ -4 & 5 \end{pmatrix} - 3 \cdot \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$
$= \begin{pmatrix} 3 - 3 & 0 \\ -4 & 5 - 3 \end{pmatrix}$
Ergebnis mit dem $\vec{x}$ multiplizieren und gleich Null setzen:
$= \begin{pmatrix} 0 & 0 \\ -4 & 2 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = 0$
$= \begin{pmatrix} 0x_1 + 0x_2 \\ -4x_1 + 2x_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$
D. h. es ist folgendes Gleichungssystem zu lösen:
$0x_1 + 0x_2 = 0$
$-4x_1 + 2x_2 = 0$ $\rightarrow x_1 = \frac{1}{2} x_2$
Da hier wieder ein Vektor $\neq 0$ resultieren muss, kann keines der beiden Werte Null werden. Denn für $x_1 = 0$ müsste $x_2$ ebenfalls gleich null sein, damit der obige Zusammenhang gegeben ist. Also setzen wir $x_1 = 1$. Das bedeutet, $x_2$ muss den Wert 2 annehmen.
Da $\vec{x} \neq \vec{0}$, ist z.B. der Vektor $x = \begin{pmatrix} 1 \\ 2 \end{pmatrix}$ ist eine Lösung des Problems, denn:
$\begin{pmatrix} 0 & 0 \\ -4 & 2 \end{pmatrix} \begin{pmatrix} 1 \\ 2 \end{pmatrix} \;$ ergibt $\; \begin{pmatrix} 0 \\ 0 \end{pmatrix}$
Weitere interessante Inhalte zum Thema
-
Eigenwerte
Vielleicht ist für Sie auch das Thema Eigenwerte (Matrizen) aus unserem Online-Kurs Analysis und Lineare Algebra interessant.