Inhaltsverzeichnis
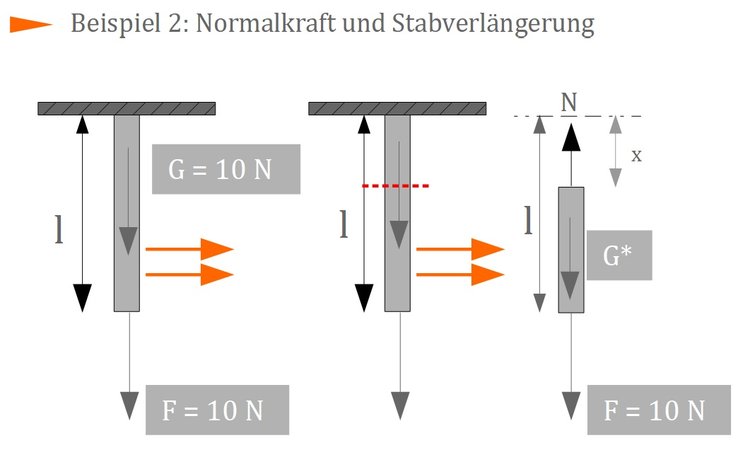
In diesem Abschnitt soll nun ein Balken mit einem Eigengewicht von $G = 10 N$ und einer am Stabende angreifenden Kraft von $F = 10 N$ betrachtet werden:
Beispiel
In der obigen Grafik ist ein eingespannter Stab aus Blei ($E = 19 \frac{kN}{mm^2}$). Der Stab besitzt ein Eigengewicht von $G = 10 N$ und wird am Ende durch eine Kraft von $F = 10 N$ belastet. Die Länge des Stabes betrage $l = 20 cm$ und die Querschnittsfläche sei $A = 50 cm^2$. Wie groß ist die Normalspannung und die Stabverlängerung?
Bestimmung der Normalspannung
Bevor die Normalspannung bestimmt werden kann, wird zunächst die Normalkraft $N(x)$ bestimmt. Hierzu wird der Balken freigeschnitten und das untere Stabelement betrachtet. Die Gewichtskraft $G*$ für dieses Stabelement muss zunächst bestimmt werden. Dies kann mittels Dreisatz durchgeführt werden:
$ G \leftrightarrow l$
$G* \leftrightarrow (l - x)$
$G* = \frac{G}{l} \cdot (l - x)$
Es kann nun mittels der vertikalen Gleichgewichtsbedingung die Normalkraft bzw. der Verlauf der Normalkraft bestimmt werden:
$\uparrow : N(x) - G* - F = 0$
$N(x) = G* + F$
$N(x) = \frac{G}{l} \cdot (l - x) + F$.
Einsetzen der Werte:
$N(x) = \frac{10 N}{20 cm} \cdot (20 cm - x) + 10 N$
$N(x) = 10 N [2 - \frac{x}{20 cm}]$
Die Normalspannung $\sigma = \frac{N}{A}$ ergibt sich dann zu:
$\sigma = \frac{10 N}{50 cm^2} [2 - \frac{x}{20 cm}]$
Methode
$\sigma = 0,2 \frac{N}{cm^2} [2 - \frac{x}{20 cm}]$
Am Stabanfang bei $x = 0$ besitzt der Stab sein Spannungsmaximum mit $\sigma = 0,4 \frac{N}{cm^2}$. Am Stabende bei $x = l = 20 cm$ besitzt der Stab eine Normalspannung von $\sigma = 0,2 \frac{N}{cm^2}$.
Vergleicht man nun die vorherigen Abschnitte, dann sollten die Spannungen an den Stabenden auch aus diesen deutlich werden. Hat der Balken nur sein Eigengewicht und keine weitere Kraft, so ist das Maximum am Stabanfang für $x = 0$ bei $\sigma = 0,2 \frac{N}{cm^2}$.
Der Balken ohne Eigengewicht aber mit Kraft am Stabende, hingegen, besitzt eine konstante Normalkraft von $\sigma = 0,2 \frac{N}{cm^2}$, also auch am Stabanfang für $x = 0$.
Nimmt man nun beide Kräfte zusammen, so ergibt sich am Stabanfang eine Normalspannung von $0,2 \frac{N}{cm^2} + 0,2 \frac{N}{cm^2} = 0,4 \frac{N}{cm^2}$. Dies entspricht genau dem oben berechneten Wert.
Das Gleiche gilt für das Stabende:
Stab nur mit Eigengewicht (x = l) : $\sigma = 0$
Stab nur mit Kraft am Stabende besitzt konstante Normalkraft: $\sigma = 0,2 \frac{N}{cm^2}$
Addition beider ergibt: $\sigma = 0,2 \frac{N}{cm^2}$
Bestimmung der Stabverlängerung
Die Stabverlängerung bestimmt sich durch:
$\triangle l = \int_0^l [\frac{N}{EA} + \alpha{_th} \triangle T] \; dx$
Da $\triangle T = 0$:
$\triangle l = \int_0^l \frac{N}{EA} \; dx$
Einsetzen von $N = N(x)$:
$\triangle l = \int_0^l [\frac{10 N}{EA} [2 - \frac{x}{20 cm}] \; dx$
$\triangle l = [\frac{10 N}{EA} (2x - \frac{x^2}{2 \cdot 20 cm})]_0^l$
$\triangle l = \frac{10 N}{EA} (2l - \frac{l^2}{2 \cdot 20 cm})$
Einsetzen der Werte:
$\triangle l = \frac{10 N}{1.900.000 \frac{N}{cm^2} \cdot 50 cm^2} (2 \cdot 20 cm - \frac{(20 cm)^2}{2 \cdot 20 cm})$
$\triangle l = 0,000003158 \; cm$.
Die Stabverlängerung beträgt demnach 0,000003158 cm. Dies entspricht genau der Zusammenfassung der vorherigen zwei Beispiele:
$\triangle l = 0,000002105 \; cm + 0,000001053 \; cm = 0,000003158 \; cm$.
Differentialgleichung des Stabes
Die Differentialgleichung des Stabes mit Linienkraft und mit angreifender Kraft sollte separat wie in den vorherigen Abschnitten betrachtet werden. Da dieses Vorgehen hier allerdings zu aufwendig ist, sollte die Bestimmung der Längenänderung wie oben bestimmt werden.
Weitere interessante Inhalte zum Thema
-
Beispiel: Belastung durch Kraft am Stabende (ohne Gewichtskraft)
Vielleicht ist für Sie auch das Thema Beispiel: Belastung durch Kraft am Stabende (ohne Gewichtskraft) (Stabbeanspruchungen) aus unserem Online-Kurs Technische Mechanik 2: Elastostatik interessant.