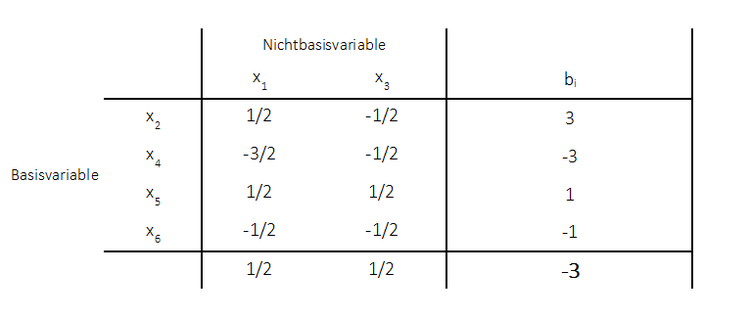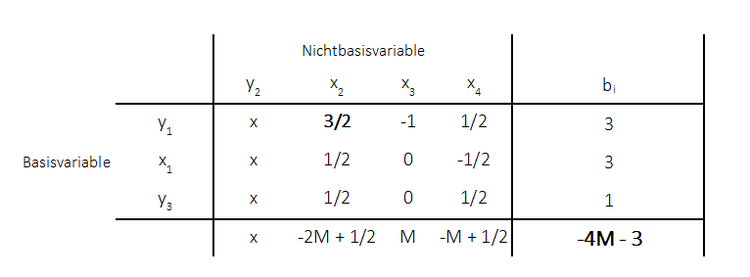Inhaltsverzeichnis
Es ist natürlich ebenfalls möglich ein gegebenes Minimierungsproblem durch bestimmte Umformumgsregeln in ein Maximierungsproblem zu transformieren und dann die Big-M-Methode bzw. den dualen Simplexalgorithmus anzuwenden ohne das Problem vorher zu dualisieren.
Umformung in Standardform (erweitert)
- Aus einem Minimierungsproblem wird ein Maximierungsproblem, indem die Zielfunktion mit $-1$ multipliziert wird.
- Ersetzen von $x_j$, welche keiner Nichtnegativitätsbedingung unterliegt, durch $x_j^+ \ge $ und $x_j^- \ge $, wobei gilt $x_j = x_j^+ - x_j^-$.
- Eine Gleichung $a_{i1}x_1 + ... + a_{in} x_n = b_i$ kann durch zwei Ungleichungen ersetzt werden
$a_{i1}x_1 + ... + a_{in} x_n = b_i$ und $-a_{i1}x_1 - ... - a_{in} x_n = -b_i$. - Aus einer $\ge$-Ungleichung wird eine $\le$-Ungleichung durch Multiplikation der gesamten Ungleichung mit $-1$.
Beispiel: Minimierungsproblem und dualer Simplexalgorithmus
Gegeben sei das folgende Minimierungsproblem:
$f(x_1, x_2) = x_1 + x_2$ $\rightarrow$ min!
u.d.N
$x_1 + 2 x_2 \ge 6$
$2x_1 + x_2 \ge 6$
$x_1 + x_2 = 4$
$x_1, x_2 \ge 0$
Das Problem wird nun zunächst auf die Standardform gebracht (Maximierungsproblem, Kleiner/Gleich-Nebenbedingung, Nichtnegativitätsbedingung):
1. Zielfunktion mit $-1$ multiplizieren:
$f(x_1, x_2) = -x_1 - x_2$ $\rightarrow$ max!
2. Nebenbedingungen mit Gleichheitszeichen in zwei Ungleichungen überführen:
$x_1 + x_2 \le 4$
$-x_1 - x_2 \le- 4$
3. Größer/Gleich-Nebenbedingungen in Kleiner/Gleich-Nebenbedingungen umformen durch Multiplikation mit $-1$:
$-x_1 - 2 x_2 \le -6$
$-2x_1 - x_2 \le -6$
Das Maximierungsproblem sieht wie folgt aus:
$f(x_1, x_2) = -x_1 - x_2$ $\rightarrow$ max!
u.d.N
$-x_1 - 2 x_2 \le -6$
$-2x_1 - x_2 \le -6$
$x_1 + x_2 \le 4$
$-x_1 - x_2 \le- 4$
$x_1, x_2 \ge 0$
Es wird anhand der Standardform nochmals geprüft, welcher Simplex hier angewandt werden kann. Der primale Simplex ist hier nicht anwendbar, da die rechte Seite negative Werte aufweist. Es kann also der duale Simplexalgorithmus angewandt werden (alternativ: Big-M-Methode). Hierzu muss das Problem aber zunächst in Normalform vorliegen:
$f(x_1, x_2) = -x_1 - x_2$ $\rightarrow$ max!
u.d.N
$-x_1 - 2 x_2 + x_3 = -6$
$-2x_1 - x_2 + x_4 = -6$
$x_1 + x_2 + x_5 = 4$
$-x_1 - x_2 + x_6 = - 4$
$x_1, x_2, x_3, x_4, x_5, x_6 \ge 0$
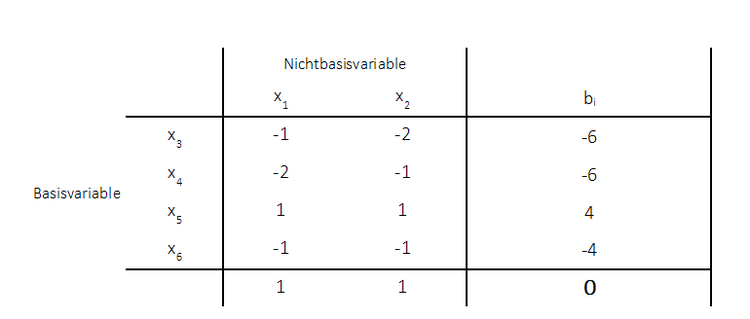
Eintragen in das Tableau:
Es kann nun der duale Simplex angewandt werden. Hierbei wird zunächst die Pivotzeile und dann die Pivotspalte ausgewählt. Es wird die Zeile als Pivotzeile gewählt, welche den kleinsten negativen Wert auf der rechten Seite aufweist. Hier existieren zwei kleinste negative Werte, es wird einer beliebig ausgewählt (1. Zeile). Es wird dann die Pivotzeile betrachtet und für alle Werte kleiner Null der Quotient aus zugehörigen Zilefunktionswert und negativen Koeffizient der Pivotzeile bestimmt:
$max \{\frac{1}{-1}; \frac{1}{-2} \} = -\frac{1}{2}$.
Es wird der größte Wert ausgewählt.
Dort wo sich Pivotspalte und Pivotzeile treffen liegt das Pivotelement, hier: $-2$. Es wird nun der Simplexschritt durchgeführt (wie beim primalen Simplexalgorithmus). Es darf nicht vergessen werden die Basisvariable und die Nichtbasisvariable des Pivotelements zu vertauschen:
Es liegt nun das folgende neue Tableau nach Durchführung eines Simplexschrittes vor. Die Vorgehensweise sei kurz zusammengefasst:
Das Pivotelement geht mit seinem reziproken Wert ein: -\frac{1}{2}$
Die neuen Elemente der Pivotzeile werden ermittelt, indem die alten Werte durch das alte Pivotelement geteilt werden.
Die neuen Elemente der Pivotspalte werden ermittelt, indem die alten Werte durch das alte Pivotelement geteilt und mit $-1$ multipliziert werden.
Die restlichen Werte werden bestimmt indem der alte Wert abzüglich der alten Werte aus zugehöriger Pivotspalte mal Pivotzeile durch Pivotelement berechnet wird. Z.B.: Der wurde der Wert $-\frac{3}{2}$ bestimmt durch:
$-2 - \frac{-1 \cdot -1}{-2}$.
Der Zielfunktionswert wurde ermittelt, indem die Basisvariablen mit den Werten der rechten Seite in die Zielfunktion eingesetzt werden (die Nichtbasisvariablen besitzen den Wert Null):
$f(x_1, x_2) = -2 \cdot 0 - 1 \cdot 3 = -3$.
Da noch immer negative Werte auf der rechten Seite vorhanden sind und damit keine zulässige Basislösung existiert (Nichtnegativitätsbedingung ist nicht gegeben, $x_4$ und $x_6$ besitzen beide einen negativen Wert), muss ein weiterer dualer Simplexschritt durchgeführt werden. Es wird wieder zunächst die Pivotzeile ausgewählt (kleinster negativer Wert der rechten Seite) und dann die Pivotspalte (nur negative Elemente der Pivotzeile werden berücksichtigt):
$max \{\frac{\frac{1}{2}}{-\frac{3}{2}}; \frac{\frac{1}{2}}{\frac{-1}{2}} \} = -\frac{1}{3}$.
Das Pivotelemt ist $-\frac{3}{2}$.
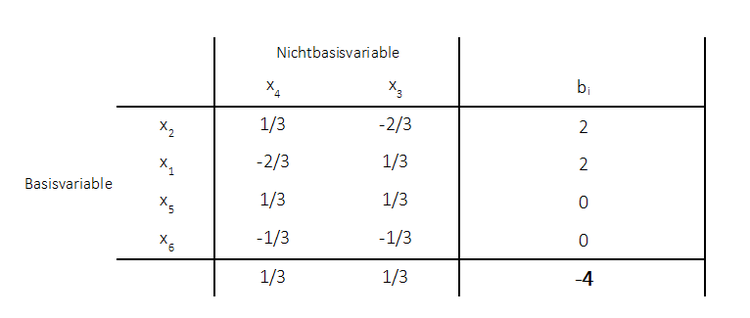
Es wird das neue Tableau aufgestellt (Nichtbasisvariable und Basisvariable vertauschen):
Es sind keine negativen Werte mehr auf der rechten Seite vorhanden. Es existiert demnach eine zulässige Lösung, weil die Nichtnegativitätsbedingung erfüllt ist. Der primale Simplex wird dann angewandet um aus der zulässigen Lösung eine optimale Lösung zu gewinnen. Da aber keine negativen Einträge in der Zielfunktionszeile vorhanden sind, ist hier bereits die optimale Lösung gegeben. Diese $x_2 = 2$ und $x_1 = 2$. Für das Maximierungsproblem gilt dann der Zielfunktionswert -4. Für das Minimierungsproblem der Zielfunktionswert $4$:
$f(x_1, x_2) = 2 + 2 = 4$
Beispiel: Minimierungsproblem und Big-M-Methode
Bei der Big-M-Methode ist es ratsam bei einer Gleichheitsbedingung im Ausgangsproblem diese nicht in zwei Ungleichungen zu überführen. Das Problem ist wie folgt gegeben:
$f(x_1, x_2) = x_1 + x_2$ $\rightarrow$ min!
u.d.N
$x_1 + 2 x_2 \ge 6$
$2x_1 + x_2 \ge 6$
$x_1 + x_2 = 4$
$x_1, x_2 \ge 0$
Das Problem wird nun in ein Maximierungsproblem mit kleiner/gleich-Nebenbedingungen umgeformt, wobei die Gleichheitsbedingung aber bestehen bleibt:
$f(x_1, x_2) = -x_1 - x_2$ $\rightarrow$ max!
u.d.N
$-x_1 - 2 x_2 \le -6$
$-2x_1 - x_2 \le -6$
$x_1 + x_2 = 4$
$x_1, x_2 \ge 0$
Das Problem wird dann in die Normalform überführt, indem die Schlupfvariablen für alle Ungleichungen eingeführt werden:
$f(x_1, x_2) = -x_1 - x_2$ $\rightarrow$ max!
u.d.N
$-x_1 - 2 x_2 + x_3 = -6$
$-2x_1 - x_2 + x_4 = -6$
$x_1 + x_2 = 4$
$x_1, x_2, x_3, x_4 \ge 0$
Danach werden alle Nebenbedingungen, für die negative Werte auf der rechten Seite vorliegen mit $-1$ multipliziert:
$f(x_1, x_2) = -x_1 - x_2$ $\rightarrow$ max!
u.d.N
$x_1 + 2 x_2 - x_3 = 6$
$2x_1 + x_2 - x_4 = 6$
$x_1 + x_2 = 4$
$x_1, x_2, x_3, x_4 \ge 0$
Es werden als nächstes künstliche Variablen für alle Nebenbedingungen mit negativen Schlupfvariablen und für alle Nebenbedingungen ohne Schlupfvariablen eingefügt. Diese werden in der Zielfunktion mit dem Wert $-M$ (wobei $M$ als hinreichend groß angenommen wird) bewertet:
$f(x_1, x_2) = -x_1 - x_2 - My_1 - My_2 - My_3$ $\rightarrow$ max!
u.d.N
$x_1 + 2 x_2 - x_3 y_1 = 6$
$2x_1 + x_2 - x_4 + y_2 = 6$
$x_1 + x_2 + y_3 = 4$
$x_1, x_2, x_3, x_4, y_1, y_2, y_3 \ge 0$
Als nächstes werden die künstlichen Variablen aus der Zielfunktion entfernt, damit diese als Basisvariablen in das Tableau eingehen. Dazu werden die Nebenbedingungen nach diesen Variablen aufgelöst und dann in die Zielfunktion eingesetzt:
$y_1 = 6 - x_1 - 2x_2 + x_3$
$y_2 = 6 - 2x_1 - x_2 + x_4$
$y_3 = 4 - x_1 - x_2 $
Einsetzen in die Zielfunktion:
$f(x_1, x_2, x_3, x_4) = -x_1 - x_2 - M(6 - x_1 - 2x_2 + x_3) - M(6 - 2x_1 - x_2 + x_4) - M( 4 - x_1 - x_2)$
Auflösen der Klammern:
$f(x_1, x_2, x_3, x_4) = -x_1 - x_2 - 6M + Mx_1 + 2Mx_2 - Mx_3 - 6M + 2Mx_1 + Mx_2 - Mx_4 - 4M + Mx_1 + Mx_2$
Zusammenfassen:
$f(x_1, x_2, x_3, x_4) = (-1 + 4M) x_1 + (-1 + 4M) x_2 - Mx_3 - Mx_4 - 16M$
Das neue Problem ergibt sich wie folgt:
$f(x_1, x_2, x_3, x_4) = (-1 + 4M) x_1 + (-1 + 4M) x_2 - Mx_3 - Mx_4 - 16M$ $\rightarrow$ max!
u.d.N
$x_1 + 2 x_2 - x_3 y_1 = 6$
$2x_1 + x_2 - x_4 + y_2 = 6$
$x_1 + x_2 + y_3 = 4$
$x_1, x_2, x_3, x_4, y_1, y_2, y_3 \ge 0$
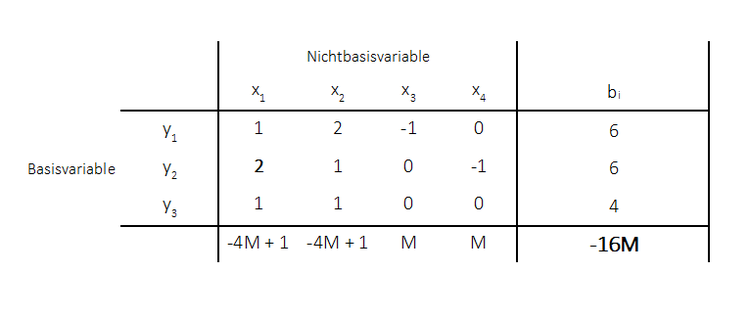
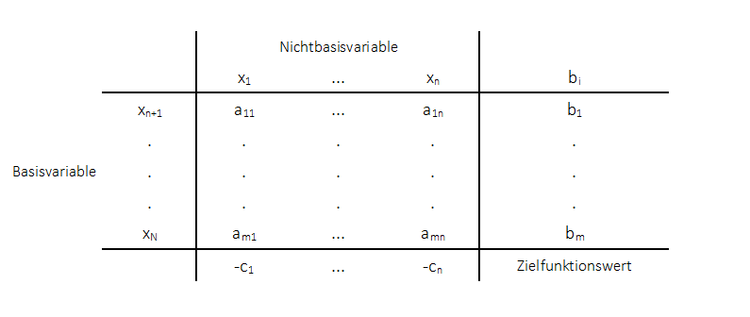
Eintragen in das Tableau:
Die Werte der Zielfunktion werden als Nichtbasisvariablen in das Ausgangstableau eingetragen. Dies sind alle Werte, die nicht mit dem Wert Null in die Zielfunktion eingehen. In diesem Fall also: $x_1, x_2, x_3, x_4$. Die Werte die nicht in der Zielfunktion auftauchen bzw. mit dem Wert Null in diese eingehen, werden in das Ausgangstableau als Basisvariablen eingetragen ($y_1 , y_2, y_3$). Die Zielfunktionswerte gehen mit ihren umgedrehten Koeffizienten in das Tableau ein:
Der Zielfunktionswert von $-16M$ ergibt sich, indem $x_1 = x_2 = x_3 = x_4 = 0$ in die Zielfunktion eingegeben werden. Da es sich hierbei um Nichtbasisvariablen handelt, besitzen diese den Wert null:
$f(x_1, x_2, x_3, x_4) = (-1 + 4M) x_1 + (-1 + 4M) x_2 - Mx_3 - Mx_4 - 16M = -16M$.
Es wird nun nach dem primalen Simplexalgorithmus vorgegangen. Das bedeutet also, dass zunächst die Pivotspalte ausgewählt wird. Hier wird der kleinste negative Koeffizient de Zielfunktionszeile gewählt. Da $M$ als hinreichend groß angenommen wird, wird sich nur an diesem Wert orientiert. Der kleinste negative Wert ist $-4M$. Es existieren zwei kleinste negative Werte. Es wird beliebig die 1. Spalte als Pivotspalte gewählt. Die Pivotzeile wird dann ermittelt, indem die Werte der rechten Seite durch die positiven Werte der Pivotspalte geteilt werden. Hierbei ist der kleinste positive Quotient zu wählen, in diesem Fall $\frac{6}{2} = 3$, also die 2. Zeile. Das Pivotelemt ist also $2$.
Es wird dann die Nichtbasisvariable $x_1$ mit der Basisvariablen $y_2$ getauscht und das neue Tableau aufgestellt indem die Simplexschritte durchgeführt werden:
In der obigen Tabellen ist das neue Tableau nach dem 1. Simplexschritt zu sehen. Die Basisvariable $y_2$ und die Nichtbasisvariable $x_1$ sind vertauscht worden. Sobald eine künstliche Variable $y_i$ die Basis verlässt und zur Nichtbasisvariable wird, kann diese im weiteren Verlauf unberücksichtigt bleiben. Dies ist anhand der $x$ angedeutet. Dies stellt auch gleichzeitig die Pivotspalte dar, welche dann für das neue Tableau nicht berechnet werden muss. Auch der Wert des alten Pivotelements muss also für das neue Tableau nicht bestimmt werden. Es müssen aber die Werte der Pivotzeile und die restlichen Werte bestimmt werden.
Werte der Pivotzeile
Der alte Wert innerhalb der Pivotzeile wird durch das Pivotelement geteilt.
Restliche Werte
Die restlichen Werte werden bestimmt indem der alte Wert abzüglich der alten Werte aus zugehöriger Pivotspalte mal Pivotzeile durch Pivotelement berechnet wird.
Der Wert $-2M + \frac{1}{2}$ wurde bestimmt durch:
$-4M + 1 - [\frac{(-4M + 1) * 1}{2}]$
$-4M + 1 - [ \frac{-4M + 1}{2}]$
$-4M + 1 - [ -2M + \frac{1}{2}]$
$-4M + 1 + 2M - \frac{1}{2}$
$-2M + \frac{1}{2}$
Zielfunktionswert
Der Zielfunktionswert wurde ermittelt, indem die Basisvariablen mit den Werten der rechten Seite in die Zielfunktion eingesetzt werden (die Nichtbasisvariablen besitzen den Wert Null):
$f(x_1, x_2, x_3, x_4) = (-1 + 4M) \cdot 3 + (-1 + 4M) \cdot 0 - M \cdot 0 - M \cdot 0 - 16M = -4M - 3$
Da noch negative Werte in der Zielfunktionszeile auftauchen ist die optimale Lösung noch nicht erreicht. Es wird ein weiterer Simplexschritt durchgeführt. Die Pivotspalte wird wieder anhand des kleinsten negativen Wertes gewählt: $-2M$. Die Pivotzeile anhand des kleinsten Quotienten (wobei nur positive Werte der Pivotspalte berücksichtigt werden dürfen). Hier besitzen die 1. und die 3. Zeile den kleinsten Quotienten. Ist dies der Fall, so wird immer diejenige Zeile bevorzugt, die eine künstliche Variable enthält (da diese in die Nichtbasis übergehen sollen). Es ist also beliebig zwischen der 1. und 3. Zeile zu wählen. Es wird im Folgenden die 1. Zeile gewählt. Das Pivotelement beträgt demnach $\frac{3}{2}$. Es wird wieder Basisvariable $y_1$ und Nichtbasisvariable $x_2$ getauscht. Die Pivotspalte (Spalte der künstlichen Variable $y_1$) bleibt für die weitere Betrachtung wieder unberücksichtigt. Es muss also nur die Pivtozeile und die restlichen Elemente berechnet werden. Es resultiert das folgende Tableau:
Der Zielfunktionswert ergibt sich durch Einfügen der Basisvariablen in die Zilefunktion (Nichtbasisvariablen nehmen den Wert null an):
$f(x_1, x_2, x_3, x_4) = (-1 + 4M) \cdot 2 + (-1 + 4M) \cdot 2 - M \cdot 0 - M \cdot 0 - 16M = 0M - 4$
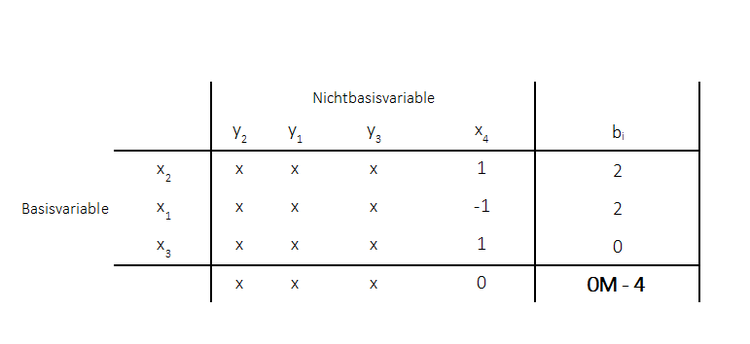
Da noch weitere negative Werte in der Zielfunktionszeile erhalten sind, wird der primale Simplexalgorithmus weiter angewandt. Die Pivotspalte kann beliebig zwischen $x_3$ und $x_4$ gewählt werden. Es wird die Spalte bei $x_3$ gewählt. Die Pivotzeile wird mit dem kleinsten Quotienten gewählt (wobei die Werte der Pivotspalte positiv sein müssen), dies entspricht hier $0$. Das Pivotelemt ist demnach $\frac{1}{3}$. Es ergibt sich das folgende Tableau:
Da keine negativen Werte mehr in der Zielfunktionszeile vorhanden sind, liegt die optimale Lösung vor. Diese beträgt mit $x_1 = 2$ und $x_2 = 2$ für das Maximierungsproblem $-4$. Für das Minimierungsproblem (Ausgangsprroblem) beträgt doe optimale Lösung dann:
$f(x_1, x_2) = 2 + 2 = 4$
Es resultiert dieselbe optimale Lösung wie bei dem dualen Simplexalgorithmus!
Merke
Das Minimierungsproblem kann auch dualsiert werden, so dass ein duales Maximierungsproblem resultiert, welches in kanonischer Form vorliegt. Es kann dann der primale Simplexalgorithmus angewandt werden, um die optimale Lösung zu erhalten.
Weitere interessante Inhalte zum Thema
-
Primales Simplexverfahren: Anfangstableau aufstellen
Vielleicht ist für Sie auch das Thema Primales Simplexverfahren: Anfangstableau aufstellen (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.
-
Umformung in die Standardform (Maximierungsproblem)
Vielleicht ist für Sie auch das Thema Umformung in die Standardform (Maximierungsproblem) (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.