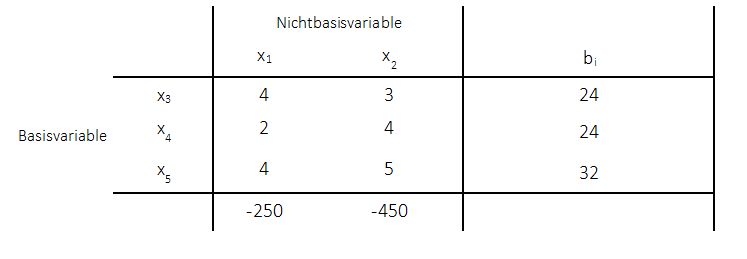Das im vorherigen Abschnitt betrachtete lineare Optimierungsproblem mit den oberen Schranken, kann auch ganz einfach mittels primalen Simplexalgorithmus gelöst werden. Dabei werden die oberen Schranken als Nebenbedingungen (so wie auch in den vorherigen Abschnitten geschehen) in das Tableau aufgenommen.
Gegeben sei das folgende Optimierungsproblem:
$f(x_1, x_2) = 2x_1 + 3x_2$ $\rightarrow$ max!
u.d.N.
$x_1 + 2x_2 \le 100$
$x_1 + x_2 \le 75$
$x_1 \le 45$
$x_2 \le 30$
$x_1, x_2 \ge 0$
Das Problem liegt in Standardform vor und die Werte der rechten Seite sind alle positiv (kanonische Form). Demnach kann hier der primale Simplexalgorithmus angewandt werden. Das Problem wird in Normalform überführt (Einfügen von Schlupfvariablen):
$f(x_1, x_2) = 2x_1 + 3x_2$ $\rightarrow$ max!
u.d.N.
$x_1 + 2x_2 + x_3 \le 100$
$x_1 + x_2 + x_4 \le 75$
$x_1 + x_5 \le 45$
$x_2 + x_6 \le 30$
$x_1, x_2, x_3, x_4, x_5, x_6 \ge 0$
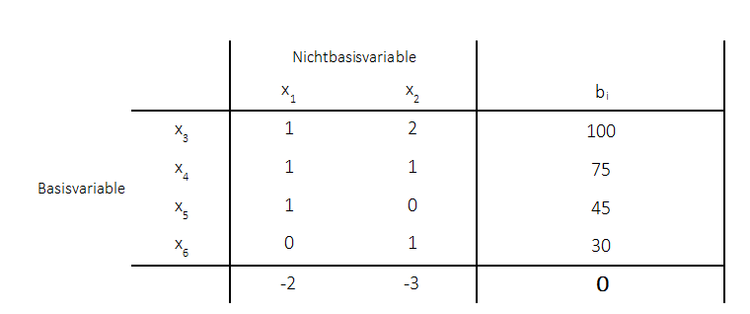
Einfügen in das Simplextableau:
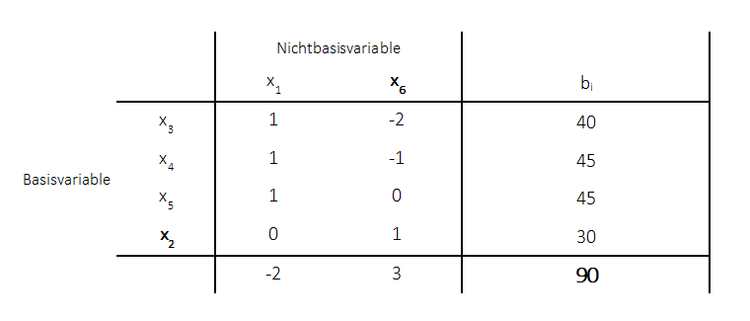
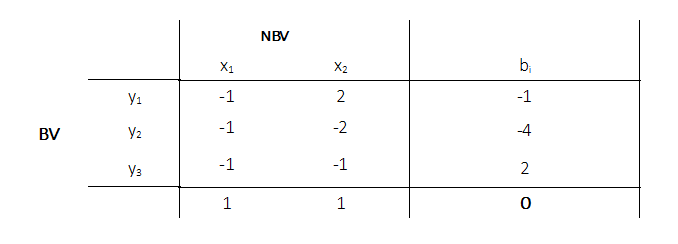
Es wird nun der primale Simplexalgorithmus angewandt. Die Vorgehensweise sollte aus den vorherigen Abschnitten bekannt sein. Es wird das Tableau nach dem 1. Simplexschritt aufgestellt:
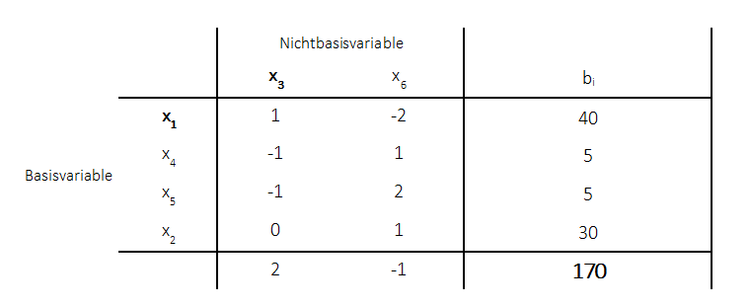
Es wird ein weiterer Simplexschritt mittels primalen Simplexalgorithmus durchgeführt. Das Tableau ergibt sich zu:
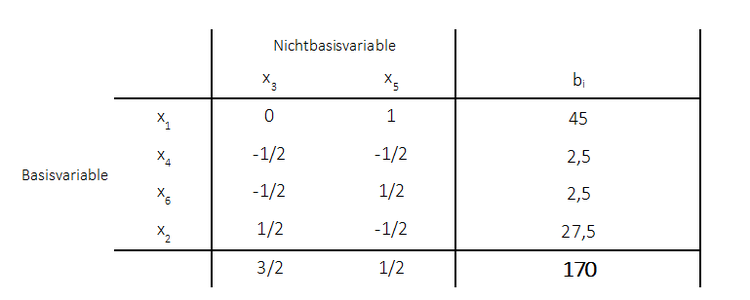
Es existiert noch ein negativer Wert in der Zielfunktionszeile. Es muss noch eine Iteration durchgeführt werden:
Das Optimaltableau ist gegeben. Der Zielfunktionswert beträgt 172,5 mit $x_1 = 45$ und $x_2 = 27,5$. Die Werte entsprechen also genau den im vorherigen Abschnitt ermittelten Werte.
Merke
Mit nur zwei Variablenbeschränkungen ist es ratsam in jedem Fall den Simplexalgorithmus anzuwenden. Die Vorgehensweise der oberen Schranken ist ratsam, wenn eine Vielzahl an Variablenbeschränkungen gegeben sind. Denn dann wird das oben durchgeführte Verfahren sehr umfangreich und unübersichtlich, da die Nebenbedingungen um die Anzahl der Variablenbeschränkungen steigen.
Weitere interessante Inhalte zum Thema
-
Dualer Simplexalgorithmus
Vielleicht ist für Sie auch das Thema Dualer Simplexalgorithmus (Grundlagen des Operations Research 1) aus unserem Online-Kurs Operations Research 2 interessant.
-
Lösung des Maximierungsproblems mittels primalen Simplexalgorithmus
Vielleicht ist für Sie auch das Thema Lösung des Maximierungsproblems mittels primalen Simplexalgorithmus (Grundlagen des Operations Research 1) aus unserem Online-Kurs Operations Research 2 interessant.