Es werden im Folgenden die Sonderfälle bei linearen Optimierungsmodellen aufgezeigt.
- Keine zulässige Lösung
Das pimale lineare Optimierungsmodell besitzt keine zulässige Lösung. Es handelt sich hierbei um eine primale Unzulässigkeit. Grund dafür sind die Nebenbedingungen, welche nicht widerspruchsfrei sind. Dieser Sonderfall tritt beim dualen Simplexalgorithmus auf. Und zwar bei Auswahl der Pivotspalte. Nachdem die Pivotzeile gewählt worden ist (kleinster negativer Wert der rechten Seite), müssen innerhalb der ausgewählten Pivotzeile Werte kleiner als Null vorhanden sein. Ist dies nicht der Fall besitzt das primale Problem keine zulässige Lösung. Das dazu duale Problem besitzt dann keine optimale Lösung.
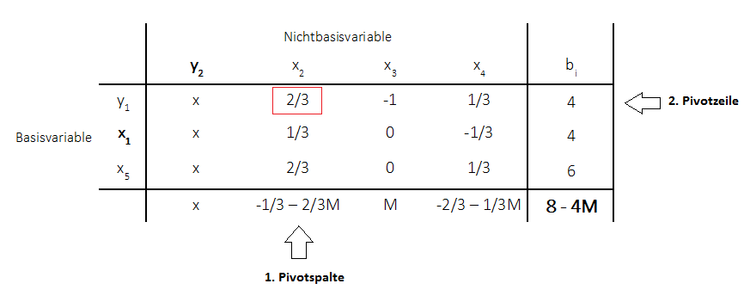
Der Sonderfall tritt bei der Big-M-Methode ein, wenn die Zielfunktionszeile positive Werte aufweist, aber immer noch künstliche Variablen $y_i$ in der Basis befinden. - Keine optimale Lösung
Das primale lineare Optimierungsmodell besitzt keine optimale Lösung. Dieser Sonderfall tritt beim primalen Simplexalgorithmus auf. Bei der Auswahl der Pivotzeile. Nachdem die Pivotspalte gewählt worden ist (kleinster negativer Wert der Zielfunktionszeile), müssen innerhalb der ausgewählten Pivotspalte Werte größer als Null vorhanden sein. Ist dies nicht der Fall, so besitzt das primale Problem keine optimale Lösung. Das dazu duale Problem besitzt dann keine zulässige Lösung. - Mehrere optimale Lösungen
Es existieren mehrere optimale Lösungen für das primale Problem. Dieser Sonderfall tritt im Optimaltableau auf (also nach Anwendung des primalen Simplexverfahrens). Existiert mindestens eine Nichtbasisvariable, welche in der Zielfunktionszeile den Wert Null aufweist, so existieren mehrere optimale Lösungen. Würde man diese Nichtbasisvariable in die Basis aufnehmen, so erhielte man eine weitere optimale Lösung. Diesen Sonderfall bezeichnet man auch als duale Degeneration, weil für das duale Problem eine Basisvariable den Wert Null annimmt (rechte Seite für diese Variable nimmt den Wert null an). - Redundante Nebenbedingung
Eine Kleiner/Gleich-Nebenbedingung ist dann redundant (überflüssig), wenn eine weitere Kleiner/Gleich-Nebenbedingung existiert, welche die selbe linke Seite aufweist, aber eine kleinere rechte Seite.
Beispiel: Die Nebenbedingung $2x_1 + x_2 \le 20$ ist redundant, wenn zusätzlich die Nebenbedingung $2x_1 + x_2 \le 10$ gegeben ist.
Eine Größer/Gleich-Nebenbedingung ist dann redundant, wenn eine weitere Größer/Gleich-Nebenbedingung exsitiert, welche die selbe linke Seite aufweist, aber eine größere rechte Seite. - Primale Degeneration
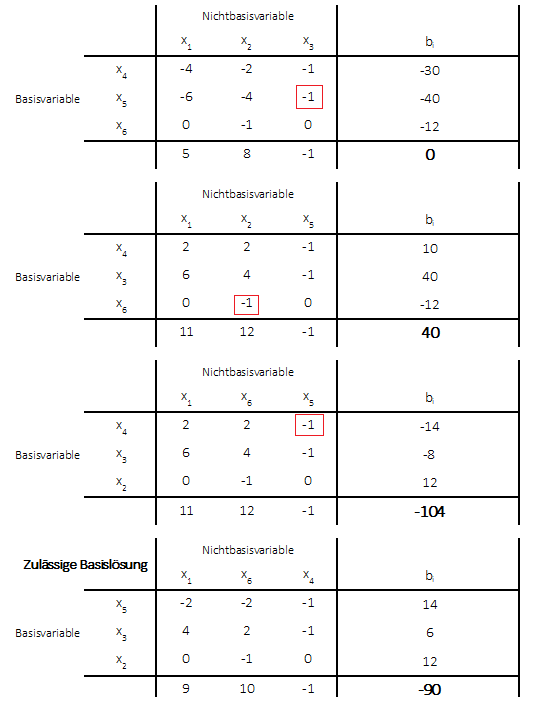
Eine primale Degeneration liegt dann vor, wenn sich im $\mathbb{R}^n$ mehr als $n$ Restriktionen in einem Punkt schneiden (grafisch erkennbar). Das bedeute also, bei Vorliegen von $n = 2$ Variablen, schneiden sich mehr als $2$ Restriktionen in einem Punkt. Für das primale Problem erkennt man die primale Degeneration Im Optimaltableau (nach Anwendung des primalen Simplexalgorithmus). Existieren dort ein oder mehere Basisvariablen mit dem Wert Null (rechte Seite), so liegt die primale Degenration vor. Für das duale Problem bedeutet dies mehrere optimale Lösungen.
Weitere interessante Inhalte zum Thema
-
Big-M-Methode: Weiterer Simplexschritt (zulässige Lösung)
Vielleicht ist für Sie auch das Thema Big-M-Methode: Weiterer Simplexschritt (zulässige Lösung) (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.
-
Beispiel: Minimierungsproblem ohne optimal Lösung
Vielleicht ist für Sie auch das Thema Beispiel: Minimierungsproblem ohne optimal Lösung (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.