Inhaltsverzeichnis
Eine Evolvente entsteht bei der Abwicklung der Evolutentangente von der Evolute. Das bedeutet also, dass die Endpunkte der Evolutentangenten in einem bestimmten Punkt die Evolvente ergeben.
Tangenten der Evoluten
Wie bereits aus den vorherigen Abschnitten bekannt, stehen Normale und Tangenten der Kurve senkrecht zueinander (im 90°-Winkel). Die Tangente der Evolute steht senkrecht (im 90°-Winkel) zur Tangente der Kurve. Daraus folgt, dass die Tangente der Evolute parallel zur Normalen der Kurve verläuft.
Merke
Die Tangente der Evolute ist gleich der Normalen der Kurve.
Dies soll anhand des Beispiels aus dem Abschnitt 'Evolute' gezeigt werden.
Anwendungsbeispiel: Tangenten der Evolute
Beispiel
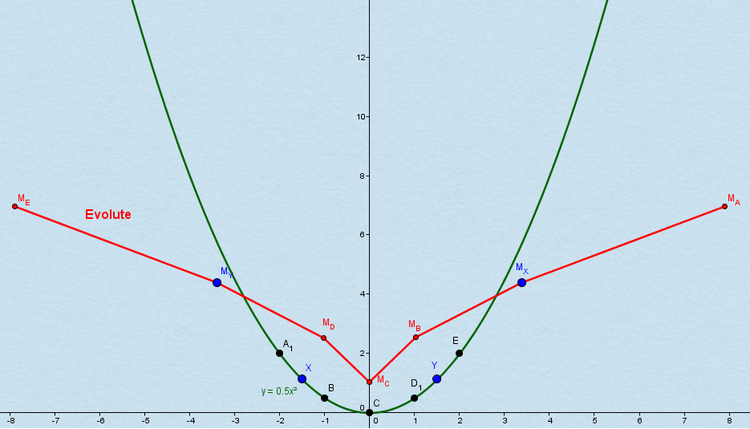
Gegeben sei die Parabel: $0,5x^2$.
Die Krümmungskreismittelpunkte wurden für verschiedene Punkte berechnet (siehe Kapitel "Evolute").
In diesem Beispiel wurden noch zwei weitere Punkte $X(-1,5, \ 1,25)$ und $Y(1,5, \ 1,25)$ eingefügt, um die Evolute genauer darzustellen. Die Evolute der Parabel sieht dann wie folgt aus:
Bestimmung des Normalenvektors
Die Tangenten der Evolute sind gleich der Normalen der Kurve.
Die Normalen der Kurve wurden bereits im Abschnitt 'Evolute' berechnet.
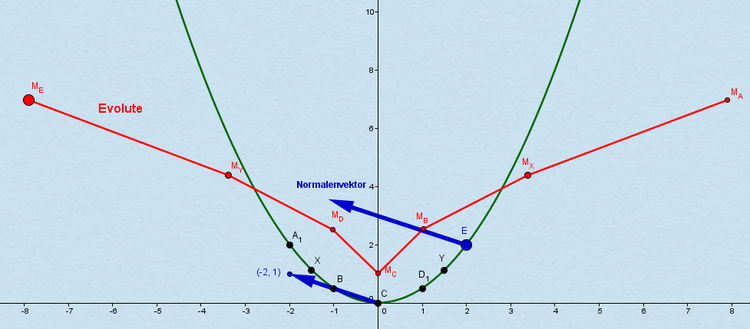
In diesem Beispiel soll es reichen einen Punkt auszuwählen und dessen Normale zu berechnen. In diesem Fall wird der Punkt $E(2, \ 2)$ dafür bestimmt. Der Normalenvektor für diesen Punkt ist:
$\vec{n} = (-f´(x), \ 1) = (-(x), \ 1) = (-2, \ 1)$
Der Normalenvektor wird an den Punkt $E$ verschoben und damit ist die Normale im Punkt $E$ ermittelt. Bis hierher ist das Vorgehen bereits aus den bisherigen Abschnitten bekannt:
Bestimmung der Evolutentangente
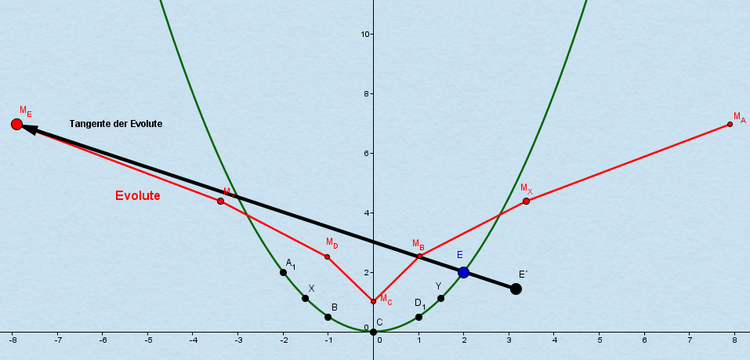
Um die Tangente der Evolute zu bestimmen wird die Normale der Parabel im Punkt $E$ bis an seinen Krümmungskreismittelpunkt $M_E$ gezogen und hinaus über den Punkt $E$.
In der Grafik ist nun die Tangente der Evolute mit ihrem Endpunkt $E´$ zu sehen. Dieser Endpunkt bildet einen Punkt auf der Evolvente. Wird nun für jeden Krümmungskreismittelpunkt auf der Evolute die Tangente bestimmt, so ergeben die Endpunkte dieser Tangenten die Evolvente.
Bestimmung der Evolvente
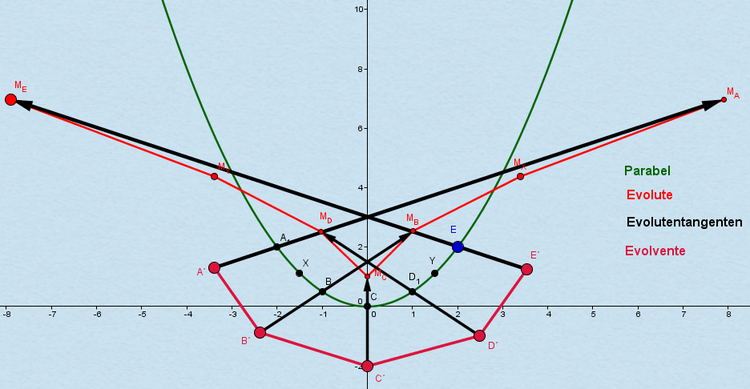
In der nachfolgenden Grafik wurde für jeden Krümmungskreismittelpunkt die Tangente gebildet und die Endpunkte der Tangente miteinander verbunden. Die Länge der Tangenten ist dabei erst einmal unerheblich. Allerdings müssen alle Tangenten von der Parabel bis zu ihrem Endpunkt den gleichen Abstand aufweisen, damit die Evolvente parallel zur Parabel verläuft. Man erhält dann EINE von unendlich vielen Evolventen. Abhängig davon wie lang die Tangenten gewählt werden, gibt es unendlich viele Evolventen die alle parallel zueinander verlaufen.
Die in der obigen Grafik ermittelte Evolvente nimmt mit zunehmender Anzahl von Krümmungskreismittelpunkten die Form der Parabel an. In diesem Beispiel ist die Evolvente ein wenig "abgehackt". Sie müsste normalerweise rundlicher verlaufen, so wie die Ausgangsparabel. Es ist aber sehr gut ersichtlich, dass die Evolvente parallel zur Parabel verläuft.
Weitere interessante Inhalte zum Thema
-
Resultierende analytisch bestimmen
Vielleicht ist für Sie auch das Thema Resultierende analytisch bestimmen (Einzelkräfte mit gemeinsamen Angriffspunkt) aus unserem Online-Kurs Technische Mechanik 1: Statik interessant.
-
Obere Schranken: Primales Simplexverfahren
Vielleicht ist für Sie auch das Thema Obere Schranken: Primales Simplexverfahren (Lineare Programmierung) aus unserem Online-Kurs Operations Research 1 interessant.